 por Mell » Qua Mai 08, 2013 00:09
por Mell » Qua Mai 08, 2013 00:09
Olá!! Resolvi o limite
![\lim_{\rightarrow\infty} \frac{\sqrt[7]{x^3-5x^2+1}}{x+3} \lim_{\rightarrow\infty} \frac{\sqrt[7]{x^3-5x^2+1}}{x+3}](/latexrender/pictures/65e1446432a7b8a9af109e806843a10c.png)
da seguinte forma:
![\lim_{\rightarrow\infty} \frac{\sqrt[7]{x^3-5x^2+1}}{x+3} \lim_{\rightarrow\infty} \frac{\sqrt[7]{x^3-5x^2+1}}{x+3}](/latexrender/pictures/65e1446432a7b8a9af109e806843a10c.png)
=
![\frac{\sqrt[7]{x^3(1-\frac{5x^2}{x^3}+\frac{1}{x^3})}}{x(1+\frac{3}{x})} \frac{\sqrt[7]{x^3(1-\frac{5x^2}{x^3}+\frac{1}{x^3})}}{x(1+\frac{3}{x})}](/latexrender/pictures/1759fbf619ba40cd40ec56849f9a5c21.png)
Considerei as parcelas
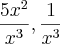
e

como limites que tendem a zero e logo ficou assim:
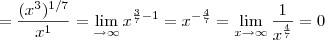
Entretanto, me falaram que o resultado da questão era +

. Só que não consigo entender porque essa minha resolução está errada... Alguém pode ajudar?? Por favor sejam gentis rs talvez meu erro esteja óbvio para alguém, mas não consigo percebê-lo.
-
Mell
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qua Mai 01, 2013 14:48
- Localização: São Paulo, SP
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por e8group » Qua Mai 08, 2013 10:34
por e8group » Qua Mai 08, 2013 10:34
Sim está correto .Não faz sentido este limite resultar
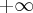
uma vez que a potência de

no denominador é estritamente maior que de

no numerador .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Mell » Qua Mai 08, 2013 18:19
por Mell » Qua Mai 08, 2013 18:19
Está certo mesmo?!! (: Ah é porque tirei essa questão de uma prova que estava corrigida como certa com o resultado +infinito... mas não vi muito sentido na resolução e tentei fazer sozinha. Obrigada pela ajuda mais uma vez!
-
Mell
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qua Mai 01, 2013 14:48
- Localização: São Paulo, SP
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por e8group » Qua Mai 08, 2013 21:21
por e8group » Qua Mai 08, 2013 21:21
Mell escreveu:Está certo mesmo?!! (: Ah é porque tirei essa questão de uma prova que estava corrigida como certa com o resultado +infinito... mas não vi muito sentido na resolução e tentei fazer sozinha. Obrigada pela ajuda mais uma vez!
De nada .Sim está correto ,caso contrário eu e vc + o site wolfram alpha estaria errado .Pois
http://www.wolframalpha.com/input/?i=li ... +infinity+ .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] limite trigonométrico quando x tende ao infinito
por Ge_dutra » Seg Jan 28, 2013 10:13
- 2 Respostas
- 7267 Exibições
- Última mensagem por Ge_dutra

Ter Jan 29, 2013 14:20
Cálculo: Limites, Derivadas e Integrais
-
- Qual o limite de [(2-x)^4-16]/x quando X tende a 0
por Therodrigou » Qua Jun 20, 2018 06:46
- 2 Respostas
- 9408 Exibições
- Última mensagem por Therodrigou

Qua Jun 20, 2018 22:54
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Questão de limite tendendo à infinito
por _bruno94 » Sex Mai 31, 2013 00:28
- 3 Respostas
- 2950 Exibições
- Última mensagem por Jhonata

Sex Mai 31, 2013 01:30
Cálculo: Limites, Derivadas e Integrais
-
- [limites no infinito]Limite no infinito de um ponto finito
por moyses » Ter Ago 30, 2011 12:45
- 3 Respostas
- 3535 Exibições
- Última mensagem por LuizAquino

Ter Ago 30, 2011 18:57
Cálculo: Limites, Derivadas e Integrais
-
- limites: tende ao infinito
por Victor Gabriel » Sáb Abr 27, 2013 00:40
- 0 Respostas
- 998 Exibições
- Última mensagem por Victor Gabriel

Sáb Abr 27, 2013 00:40
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{\rightarrow\infty} \frac{\sqrt[7]{x^3-5x^2+1}}{x+3} \lim_{\rightarrow\infty} \frac{\sqrt[7]{x^3-5x^2+1}}{x+3}](/latexrender/pictures/65e1446432a7b8a9af109e806843a10c.png) da seguinte forma:
da seguinte forma:![\lim_{\rightarrow\infty} \frac{\sqrt[7]{x^3-5x^2+1}}{x+3} \lim_{\rightarrow\infty} \frac{\sqrt[7]{x^3-5x^2+1}}{x+3}](/latexrender/pictures/65e1446432a7b8a9af109e806843a10c.png) =
=![\frac{\sqrt[7]{x^3(1-\frac{5x^2}{x^3}+\frac{1}{x^3})}}{x(1+\frac{3}{x})} \frac{\sqrt[7]{x^3(1-\frac{5x^2}{x^3}+\frac{1}{x^3})}}{x(1+\frac{3}{x})}](/latexrender/pictures/1759fbf619ba40cd40ec56849f9a5c21.png) Considerei as parcelas
Considerei as parcelas 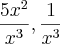 e
e  como limites que tendem a zero e logo ficou assim:
como limites que tendem a zero e logo ficou assim: 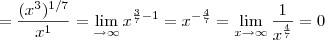
 . Só que não consigo entender porque essa minha resolução está errada... Alguém pode ajudar?? Por favor sejam gentis rs talvez meu erro esteja óbvio para alguém, mas não consigo percebê-lo.
. Só que não consigo entender porque essa minha resolução está errada... Alguém pode ajudar?? Por favor sejam gentis rs talvez meu erro esteja óbvio para alguém, mas não consigo percebê-lo.

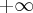 uma vez que a potência de
uma vez que a potência de  no denominador é estritamente maior que de
no denominador é estritamente maior que de 

 .
.
 :
: