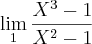
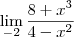
Se conseguirem o 1ª exercício,acho que daria pra fazer o 2ª exercício !
E este aqui :
![\lim_{9}\frac{ \sqrt[]{x}-3}{x^2-9x} \lim_{9}\frac{ \sqrt[]{x}-3}{x^2-9x}](/latexrender/pictures/c09f7be5ad5b10ce05a0fbff1417c665.png)
Este terceiro eu não consigo também .
Se alguém puder me ajudar eu fico grato.

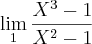
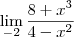
![\lim_{9}\frac{ \sqrt[]{x}-3}{x^2-9x} \lim_{9}\frac{ \sqrt[]{x}-3}{x^2-9x}](/latexrender/pictures/c09f7be5ad5b10ce05a0fbff1417c665.png)

 é raiz de
é raiz de 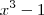 e
e 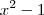 e portanto podemos dividir ambas expressões por
e portanto podemos dividir ambas expressões por  para fatorá-las . De forma análoga ,podemos fatorar
para fatorá-las . De forma análoga ,podemos fatorar 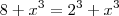 e
e  ao dividirmos ambas expressões por
ao dividirmos ambas expressões por  (Por quê ???) .No último exercício o argumento é semelhante e ainda acrescento uma dica para ele , deixe o "x" em evidência no denominador (Veja que
(Por quê ???) .No último exercício o argumento é semelhante e ainda acrescento uma dica para ele , deixe o "x" em evidência no denominador (Veja que ![x^2- 9x = x[x -9] x^2- 9x = x[x -9]](/latexrender/pictures/e78f330a167c7c406ab12a4f7416a4e3.png) )
)
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)