 por marcosmuscul » Qui Abr 04, 2013 14:54
por marcosmuscul » Qui Abr 04, 2013 14:54
-
marcosmuscul
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Ter Mar 19, 2013 15:48
- Localização: RJ
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: a começar engenharia civil
- Andamento: cursando
 por Russman » Qui Abr 04, 2013 16:30
por Russman » Qui Abr 04, 2013 16:30
A sua derivada não está correta. falta multiplicar um dos
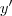
por

.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por marcosmuscul » Qui Abr 04, 2013 17:40
por marcosmuscul » Qui Abr 04, 2013 17:40
valeu
-
marcosmuscul
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Ter Mar 19, 2013 15:48
- Localização: RJ
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: a começar engenharia civil
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Calcular coeficiente angular e equação da reta tangente
por Reh » Qua Jul 20, 2016 18:52
- 4 Respostas
- 7820 Exibições
- Última mensagem por Reh

Sex Jul 22, 2016 08:58
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas]Eq da reta tangente e normal
por may » Ter Mai 14, 2013 04:41
- 1 Respostas
- 2070 Exibições
- Última mensagem por adauto martins

Qua Out 15, 2014 21:02
Cálculo: Limites, Derivadas e Integrais
-
- Calcular reta tangente e normal à curva
por Kingflare » Dom Dez 07, 2014 23:54
- 1 Respostas
- 2699 Exibições
- Última mensagem por Molina

Qua Dez 17, 2014 14:15
Cálculo: Limites, Derivadas e Integrais
-
- TRAÇAR O GRÁFICO DA RETA TANGENTE
por ton_cineasta » Qui Abr 05, 2018 18:26
- 2 Respostas
- 6999 Exibições
- Última mensagem por ton_cineasta

Seg Abr 09, 2018 15:47
Cálculo: Limites, Derivadas e Integrais
-
- Derivada reta tangente ao gráfico
por Carolminera » Dom Jul 06, 2014 16:53
- 1 Respostas
- 2634 Exibições
- Última mensagem por e8group

Dom Jul 06, 2014 20:11
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

![2x - \left(\sqrt[2]{xy} + x\left(\frac{\left(y\prime + x \right)}{2\sqrt[2]{xy}} \right)\right) + 4yy\prime = 0 2x - \left(\sqrt[2]{xy} + x\left(\frac{\left(y\prime + x \right)}{2\sqrt[2]{xy}} \right)\right) + 4yy\prime = 0](/latexrender/pictures/1b28660e2d5efa623cdd76f28645f3c7.png)
![y\prime\left(4y - \frac{x}{2\sqrt[2]{xy}} \right) = -2x + \sqrt[2]{xy} + \frac{{x}^{2}}{2\sqrt[2]{xy}} y\prime\left(4y - \frac{x}{2\sqrt[2]{xy}} \right) = -2x + \sqrt[2]{xy} + \frac{{x}^{2}}{2\sqrt[2]{xy}}](/latexrender/pictures/877abdcfae1daeb37d9d09f2ebc3eaa5.png)
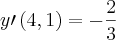



![2x - \left(\sqrt[2]{xy} + x\left(\frac{\left(y\prime + x \right)}{2\sqrt[2]{xy}} \right)\right) + 4yy\prime = 0 2x - \left(\sqrt[2]{xy} + x\left(\frac{\left(y\prime + x \right)}{2\sqrt[2]{xy}} \right)\right) + 4yy\prime = 0](/latexrender/pictures/1b28660e2d5efa623cdd76f28645f3c7.png)
![y\prime\left(4y - \frac{x}{2\sqrt[2]{xy}} \right) = -2x + \sqrt[2]{xy} + \frac{{x}^{2}}{2\sqrt[2]{xy}} y\prime\left(4y - \frac{x}{2\sqrt[2]{xy}} \right) = -2x + \sqrt[2]{xy} + \frac{{x}^{2}}{2\sqrt[2]{xy}}](/latexrender/pictures/877abdcfae1daeb37d9d09f2ebc3eaa5.png)


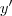 por
por  .
.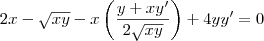


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
