 por samysoares » Ter Fev 26, 2013 13:11
por samysoares » Ter Fev 26, 2013 13:11
-
samysoares
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Ter Jan 08, 2013 12:42
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Jhonata » Ter Fev 26, 2013 13:47
por Jhonata » Ter Fev 26, 2013 13:47
samysoares escreveu:![\lim_{x\rightarrow2} \frac{tg2(x-2)}{\sqrt[]{x+2}-2} \lim_{x\rightarrow2} \frac{tg2(x-2)}{\sqrt[]{x+2}-2}](/latexrender/pictures/829953c2b59bddc32b43b0ca154ba37b.png)
Sugestão: Trate
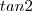
como uma constante e passe o limite, assim:
![tan2 \lim_{x\rightarrow2} \frac{(x-2)}{\sqrt[]{x+2}-2} tan2 \lim_{x\rightarrow2} \frac{(x-2)}{\sqrt[]{x+2}-2}](/latexrender/pictures/08b7f7233256555befb89b132d8fa814.png)
. Tente resolver esse limite, se não conseguir, poste sua dúvida. ;D
Abraços.
" A Matemática é a honra do espírito humano - Leibniz "
-
Jhonata
- Usuário Parceiro

-
- Mensagens: 66
- Registrado em: Sáb Mai 26, 2012 17:42
- Localização: Rio de Janeiro
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenheria Mecânica - UFRJ
- Andamento: cursando
 por samysoares » Ter Fev 26, 2013 14:20
por samysoares » Ter Fev 26, 2013 14:20
consegui. Muito obrigada. Você poderia me dizer em quais casos eu faço subsituição por outra variável, ou eu tenho que analisar cada caso?
-
samysoares
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Ter Jan 08, 2013 12:42
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Jhonata » Ter Fev 26, 2013 14:29
por Jhonata » Ter Fev 26, 2013 14:29
samysoares escreveu:consegui. Muito obrigada. Você poderia me dizer em quais casos eu faço subsituição por outra variável, ou eu tenho que analisar cada caso?
Em limites no cálculo I, particularmente, não existem regras especificas pra substituição. Acho dependerá de cada caso pra substituir a variável e calcular assim um novo limite.
Abraços.
" A Matemática é a honra do espírito humano - Leibniz "
-
Jhonata
- Usuário Parceiro

-
- Mensagens: 66
- Registrado em: Sáb Mai 26, 2012 17:42
- Localização: Rio de Janeiro
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenheria Mecânica - UFRJ
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite trigonométrico] Como calculo este limite?
por Ronaldobb » Qua Nov 07, 2012 23:14
- 3 Respostas
- 5125 Exibições
- Última mensagem por Ronaldobb

Qui Nov 08, 2012 07:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] limite trigonométrico quando x tende ao infinito
por Ge_dutra » Seg Jan 28, 2013 10:13
- 2 Respostas
- 7267 Exibições
- Última mensagem por Ge_dutra

Ter Jan 29, 2013 14:20
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] calculo de limite trigonométrico
por PRADO » Dom Mai 22, 2016 17:01
- 2 Respostas
- 5630 Exibições
- Última mensagem por PRADO

Sex Jun 03, 2016 23:25
Cálculo: Limites, Derivadas e Integrais
-
- [Limite trigonométrico]
por Ana_Rodrigues » Qui Jan 26, 2012 18:54
- 4 Respostas
- 2860 Exibições
- Última mensagem por Ana_Rodrigues

Sex Jan 27, 2012 14:28
Cálculo: Limites, Derivadas e Integrais
-
- Limite trigonométrico
por jmoura » Dom Mar 25, 2012 21:25
- 2 Respostas
- 2074 Exibições
- Última mensagem por LuizAquino

Seg Mar 26, 2012 13:02
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x\rightarrow2} \frac{tg2(x-2)}{\sqrt[]{x+2}-2} \lim_{x\rightarrow2} \frac{tg2(x-2)}{\sqrt[]{x+2}-2}](/latexrender/pictures/829953c2b59bddc32b43b0ca154ba37b.png)



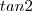 como uma constante e passe o limite, assim:
como uma constante e passe o limite, assim:![tan2 \lim_{x\rightarrow2} \frac{(x-2)}{\sqrt[]{x+2}-2} tan2 \lim_{x\rightarrow2} \frac{(x-2)}{\sqrt[]{x+2}-2}](/latexrender/pictures/08b7f7233256555befb89b132d8fa814.png) . Tente resolver esse limite, se não conseguir, poste sua dúvida. ;D
. Tente resolver esse limite, se não conseguir, poste sua dúvida. ;D


![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)