 por manuel_pato1 » Qui Jan 03, 2013 17:48
por manuel_pato1 » Qui Jan 03, 2013 17:48
Olá pessoal, sem querer ser repetitivo em criar tópicos para cada integral dessa minha dúvida, postarei as 3 nesse tópico, ok?
a)
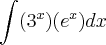
b)
![\int 15x^4/ \sqrt[]{1-x^10}dx \int 15x^4/ \sqrt[]{1-x^10}dx](/latexrender/pictures/60ef595aa823896d449e5ee9c7dde093.png)
( x elevado na 10)
c)
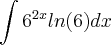
na letra A , tentei chamar u=x, logo, du=dx... que com os ajustes, me resultou em :
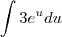
... mas a resposta daria
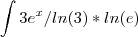
, porém a resposta correta é 3e^x/ln(3) + 1
na letra B, o x elevado na 10, eu separei em (x^2)*(x^2)*(x^2)*(x^2)*(x^2) e tirei da raíz ficando x^4 multiplicando a raiz de 1 - x^2... Aí cortei o x^4 que eu tirei da raiz com o x^4 que multiplica o 15 no numerador, enfim... a resposta que cheguei foi 15 arc sin(x) + c e no gabarito é: 3arc sin(X/5)
na letra C, eu realmente não sei começar essa , mas a respota correta é (6^2x)/2 + C
----------------------------------------------------
Desde já, muito obrigado
-
manuel_pato1
- Usuário Dedicado

-
- Mensagens: 33
- Registrado em: Ter Set 18, 2012 22:18
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por Russman » Qui Jan 03, 2013 18:33
por Russman » Qui Jan 03, 2013 18:33
Sempre que você se deparar com esses produtos
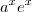
em integrais tente colocá-lo em uma unica base, no caso a base

.
Use a identidade
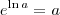
de forma que

. Assim:
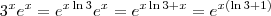
.
Agora temos uma integral na forma
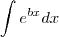
onde

é uma constante e, no caso,
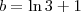
. Agora, faça
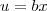
de forma que
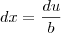
e então
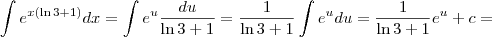
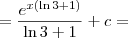
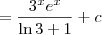
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por ant_dii » Sáb Jan 05, 2013 15:20
por ant_dii » Sáb Jan 05, 2013 15:20
Na segunda (b) você poderá fazer o seguinte:
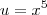
de onde
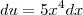
... Assim o termo do numerador de

sumirá e o termo de
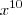
do binômio dentro da raiz poderá ser escrita como
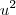
... Agora basta continuar...
O terceiro (c) faça
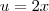
... logo você terá
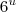
... a integral de
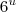
é
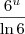
... Continue agora.
Qualquer coisa, estamos a disposição...
Só os loucos sabem...
-
ant_dii
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qua Jun 29, 2011 19:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
 por manuel_pato1 » Ter Jan 08, 2013 15:56
por manuel_pato1 » Ter Jan 08, 2013 15:56
Caras, aos dois, muito obrigado pelas respostas muito didáticas. Consegui resolver as três graças aos seus auxílios. Abração
-
manuel_pato1
- Usuário Dedicado

-
- Mensagens: 33
- Registrado em: Ter Set 18, 2012 22:18
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integrais indefinidas e definidas
por Rose » Qui Abr 23, 2009 11:18
- 2 Respostas
- 5244 Exibições
- Última mensagem por Rose

Qui Abr 23, 2009 16:43
Cálculo: Limites, Derivadas e Integrais
-
- Integrais Indefinidas e definidas 2°EM
por Beik » Sex Out 22, 2010 13:39
- 4 Respostas
- 3243 Exibições
- Última mensagem por Beik

Sáb Out 23, 2010 10:27
Cálculo: Limites, Derivadas e Integrais
-
- DUVIDA EM INTEGRAIS INDEFINIDAS
por Claytonc » Ter Jun 07, 2011 22:16
- 3 Respostas
- 3731 Exibições
- Última mensagem por LuizAquino

Qua Jun 08, 2011 15:53
Cálculo
-
- Integral indefinidas:
por Dethe » Qua Dez 15, 2010 20:48
- 2 Respostas
- 4624 Exibições
- Última mensagem por teabiofeul

Seg Out 05, 2015 08:42
Mensagens Matemáticas
-
- [integrais] Calculando áreas - Integrais
 por Faby » Seg Set 19, 2011 10:55
por Faby » Seg Set 19, 2011 10:55
- 11 Respostas
- 8859 Exibições
- Última mensagem por LuizAquino

Qua Set 21, 2011 18:03
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
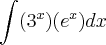
![\int 15x^4/ \sqrt[]{1-x^10}dx \int 15x^4/ \sqrt[]{1-x^10}dx](/latexrender/pictures/60ef595aa823896d449e5ee9c7dde093.png) ( x elevado na 10)
( x elevado na 10)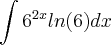
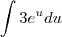 ... mas a resposta daria
... mas a resposta daria 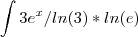 , porém a resposta correta é 3e^x/ln(3) + 1
, porém a resposta correta é 3e^x/ln(3) + 1

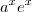 em integrais tente colocá-lo em uma unica base, no caso a base
em integrais tente colocá-lo em uma unica base, no caso a base  .
.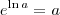 de forma que
de forma que  . Assim:
. Assim: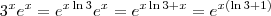 .
.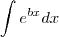 onde
onde  é uma constante e, no caso,
é uma constante e, no caso, 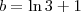 . Agora, faça
. Agora, faça 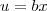 de forma que
de forma que 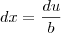 e então
e então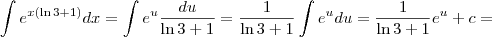
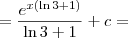
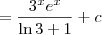

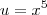 de onde
de onde 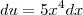 ... Assim o termo do numerador de
... Assim o termo do numerador de  sumirá e o termo de
sumirá e o termo de 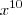 do binômio dentro da raiz poderá ser escrita como
do binômio dentro da raiz poderá ser escrita como 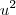 ... Agora basta continuar...
... Agora basta continuar...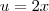 ... logo você terá
... logo você terá 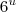 ... a integral de
... a integral de 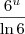 ... Continue agora.
... Continue agora.