minha resposta:
como a reta parte da origem, temos que, O = (0,0) e portanto a variação do x é de 0 até 1.
coomo o x e o y são sempre iguais, eu tirei que a função é y=x.
a fórmula a ser usade é:
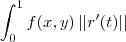
vamos aos cálculos
como o y= x temos que o vetor posição é
r(t) xi+xj
(obs. se puder explicar melhor como encontro o vetor posição, eu fico muito grato.)
Agora o vetor tangente:
r'(t)= 1i + 0j
a norma de r'(t)=
![||r'(t)|| = \sqrt[]{ {(1i)}^{2} + {(0j)}^{2} } ||r'(t)|| = \sqrt[]{ {(1i)}^{2} + {(0j)}^{2} }](/latexrender/pictures/e476fdd05df5c7c01ea3d83cf7419532.png) = 1
= 1agora vou substituir y=x na densidade, obtendo: 3xx = 3x²
calculando a integral:
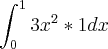
![\frac{3}{3} \left[{x}^{3} \right] \frac{3}{3} \left[{x}^{3} \right]](/latexrender/pictures/dd4024288e61c68b5b1f0e27c4e46710.png)
1*1³=1 <==Resposta.
Obrigado pela atenção.


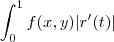


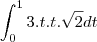
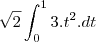
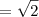


 .
.
 :
: