 por lhol » Ter Nov 13, 2012 13:26
por lhol » Ter Nov 13, 2012 13:26
Boa Tarde. Galera. Tenho uma eq diff e não entendi a resolução do wolfram alpha. é dado que y(0)= 5

-
lhol
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Ter Nov 13, 2012 13:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por MarceloFantini » Ter Nov 13, 2012 20:42
por MarceloFantini » Ter Nov 13, 2012 20:42
Acredito que seja possível resolver por separação de variáveis:

, daí

.
Integrando de ambos lados, temos

e

.
Usando a condição de contorno temos que

, portanto

.
Finalmente,
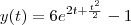
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por lhol » Ter Nov 13, 2012 23:46
por lhol » Ter Nov 13, 2012 23:46
O meu problema era com a relacao ln e e, mas entendi vlw
-
lhol
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Ter Nov 13, 2012 13:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação Diferencial.
por Higor » Seg Fev 21, 2011 13:12
- 4 Respostas
- 12218 Exibições
- Última mensagem por Higor

Seg Fev 21, 2011 14:46
Cálculo: Limites, Derivadas e Integrais
-
- Equaçao diferencial
por romulo39 » Dom Abr 03, 2011 20:58
- 1 Respostas
- 3944 Exibições
- Última mensagem por LuizAquino

Seg Abr 04, 2011 14:39
Cálculo: Limites, Derivadas e Integrais
-
- Equação diferencial
por jacquelline » Qui Mai 17, 2012 11:04
- 2 Respostas
- 2078 Exibições
- Última mensagem por jacquelline

Sáb Mai 19, 2012 20:37
Cálculo: Limites, Derivadas e Integrais
-
- Equação diferencial - 1
por Cleyson007 » Qua Nov 07, 2012 21:09
- 8 Respostas
- 3857 Exibições
- Última mensagem por MarceloFantini

Qui Nov 08, 2012 17:05
Cálculo: Limites, Derivadas e Integrais
-
- Equação diferencial - 2
por Cleyson007 » Qua Nov 07, 2012 21:14
- 1 Respostas
- 1489 Exibições
- Última mensagem por e8group

Qua Nov 14, 2012 10:06
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





 , daí
, daí  .
. e
e  .
. , portanto
, portanto .
.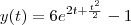 .
.

