1) Pontos minimos e/ou maximos
2) A concavidade é voltada para cima ou para baixo? diga os intervalos que isso acontece.

Sou usuário frequente do forum, e sei que precisa dizer até aonde chegou, mas eu me confudi todo e fiz de varias formas.
obs: se tiver algum erro no enunciado, por favor me avise, pois não me lembro 100%.
O primeiro passo é derivar, fica
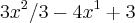 , tu considera a derivada como f'(x), a partir dai, não sei se faço f'(x)=0 ou se f'(0), preciso fazer o quadro dos sinais?
, tu considera a derivada como f'(x), a partir dai, não sei se faço f'(x)=0 ou se f'(0), preciso fazer o quadro dos sinais?alguém poderia me ajudar?
obrigado!
----
editado:
Utilizando uma sugestão do forum fiz o grafico pelo: http://www.wolframalpha.com/input/?i=x% ... 2+%2B3x+-1, então acredito que acertei meu passo até descobrir as raizes da derivada, dando os pontos minimo 1 e ponto maximo 3.... So que a partir dai, comecei a tentar testar fazendo substituição e comecei a errar, dai não consegui chegar aos resultados.


