 por Thyago Quimica » Sáb Set 22, 2012 13:12
por Thyago Quimica » Sáb Set 22, 2012 13:12
1)
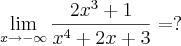
Eu sei que....
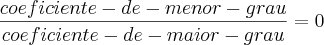
mais como desenvolver a conta para se chegar ao resultado? Coloquei os de maior em evidencia.. mas nao consegui chegar ao resultado 0 @1!
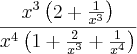
Deste ja agradeço a quem poder responder !!
Editado pela última vez por
Thyago Quimica em Sáb Set 22, 2012 15:33, em um total de 2 vezes.
-
Thyago Quimica
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Sáb Mai 05, 2012 17:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Química
- Andamento: cursando
 por MarceloFantini » Sáb Set 22, 2012 13:56
por MarceloFantini » Sáb Set 22, 2012 13:56
Prezado
Thiago,
Por favor, antes de postar um tópico leia as
Regras deste Fórum. Em especial, vide a regra 5.
O seu tópico não deverá ser respondido antes de estar de acordo com as regras.
Atenciosamente,
Equipe de ModeradoresFuturo MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- limite da divisão de dois polinomios ,sem usar l'hopital
por nandooliver008 » Ter Set 09, 2014 15:59
- 1 Respostas
- 1658 Exibições
- Última mensagem por young_jedi

Qui Set 11, 2014 10:04
Cálculo: Limites, Derivadas e Integrais
-
- [Polinômios] Grau do Polinômios e +
por Warioboy » Ter Mai 29, 2012 15:06
- 5 Respostas
- 8376 Exibições
- Última mensagem por Cleyson007

Dom Jun 03, 2012 16:18
Polinômios
-
- Polinômios
por Rose » Seg Set 08, 2008 22:07
- 2 Respostas
- 4654 Exibições
- Última mensagem por Rose

Qua Set 10, 2008 11:50
Polinômios
-
- Polinômios - 3
por DanielFerreira » Ter Set 22, 2009 13:59
- 3 Respostas
- 3084 Exibições
- Última mensagem por DanielFerreira

Qui Fev 10, 2011 09:26
Polinômios
-
- Polinômios - 2
por DanielFerreira » Ter Set 22, 2009 14:00
- 1 Respostas
- 3250 Exibições
- Última mensagem por thadeu

Seg Nov 02, 2009 11:47
Polinômios
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
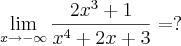
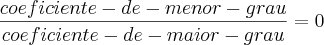
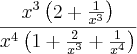

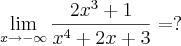
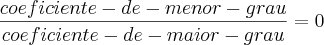
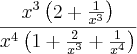



 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.