 por Caliani » Sáb Set 15, 2012 17:38
por Caliani » Sáb Set 15, 2012 17:38
Enunciado do exercício:
7. Determine se existe cada um dos limites abaixo. Justifique a existência ou não existência de cada um e determine o valor dos que existem.
(f)
![\lim_{(x,y)\rightarrow(0,0)} \frac{1 - \sqrt[]{1-{x}^{2}-{y}^{2}}}{{x}^{2}+{y}^{2}} \lim_{(x,y)\rightarrow(0,0)} \frac{1 - \sqrt[]{1-{x}^{2}-{y}^{2}}}{{x}^{2}+{y}^{2}}](/latexrender/pictures/91de2e2980a7ae8d78ce5d6a5f1726f0.png)
Eu sinceramente não sei o que fazer. Fiz
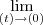
em f(t,0) e f(0,t), e depois tentei usar L'Hôpital, mas tenho problemas pra derivar o que sobra.
Alguém tem alguma ideia do que é preciso fazer? Agradeço desde já.
-
Caliani
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Set 15, 2012 17:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Economia
- Andamento: cursando
 por MarceloFantini » Sáb Set 15, 2012 19:11
por MarceloFantini » Sáb Set 15, 2012 19:11
Note que
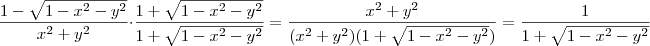
.
Logo, aplicando o limite temos que
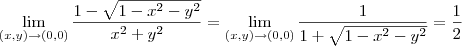
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Caliani » Sáb Set 15, 2012 20:38
por Caliani » Sáb Set 15, 2012 20:38
Muito obrigado!
-
Caliani
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Set 15, 2012 17:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Economia
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] Problema de Limite.
por ArthurNaro » Qua Jul 09, 2014 21:34
- 1 Respostas
- 1066 Exibições
- Última mensagem por e8group

Qui Jul 10, 2014 00:57
Cálculo: Limites, Derivadas e Integrais
-
- Limite Trigonométrico [Problema com o Zero]
 por LukasTsunami » Qui Out 09, 2014 14:58
por LukasTsunami » Qui Out 09, 2014 14:58
- 1 Respostas
- 986 Exibições
- Última mensagem por adauto martins

Sáb Out 11, 2014 14:29
Cálculo: Limites, Derivadas e Integrais
-
- [limite] problema com a minha resolução
por Henrique Bueno » Ter Abr 17, 2012 18:35
- 1 Respostas
- 1516 Exibições
- Última mensagem por fraol

Ter Abr 17, 2012 22:35
Cálculo: Limites, Derivadas e Integrais
-
- [limite polinomial] Problema com fatoração
por ZANGARO » Qui Mar 28, 2013 18:53
- 4 Respostas
- 3355 Exibições
- Última mensagem por ZANGARO

Sex Mar 29, 2013 01:10
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Gráfico e limite para função maior inteiro
 por Raphaela_sf » Qui Abr 05, 2012 19:26
por Raphaela_sf » Qui Abr 05, 2012 19:26
- 1 Respostas
- 6480 Exibições
- Última mensagem por LuizAquino

Qui Abr 05, 2012 20:53
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 11 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
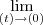 em f(t,0) e f(0,t), e depois tentei usar L'Hôpital, mas tenho problemas pra derivar o que sobra.
em f(t,0) e f(0,t), e depois tentei usar L'Hôpital, mas tenho problemas pra derivar o que sobra. 
![\lim_{(x,y)\rightarrow(0,0)} \frac{1 - \sqrt[]{1-{x}^{2}-{y}^{2}}}{{x}^{2}+{y}^{2}} \lim_{(x,y)\rightarrow(0,0)} \frac{1 - \sqrt[]{1-{x}^{2}-{y}^{2}}}{{x}^{2}+{y}^{2}}](/latexrender/pictures/91de2e2980a7ae8d78ce5d6a5f1726f0.png)

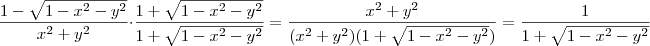 .
. 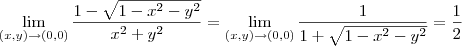 .
.

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.