 por Thyago Quimica » Qui Mai 24, 2012 17:44
por Thyago Quimica » Qui Mai 24, 2012 17:44
1)
![\lim_{x\rightarrow+\infty}\left[{2}^{x}-{3}^{x} \right] \lim_{x\rightarrow+\infty}\left[{2}^{x}-{3}^{x} \right]](/latexrender/pictures/11a0c5ea6f36a9873525a8bd84161338.png)
2)

tendei fazer pelas propriedades mais o meu resultado nao bate, que deveria ser

e

-
Thyago Quimica
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Sáb Mai 05, 2012 17:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Química
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [LIMITE]LIMITE FUNDAMENTAL EXPONENCIAL
por beel » Sáb Set 03, 2011 22:11
- 3 Respostas
- 2393 Exibições
- Última mensagem por beel

Dom Set 04, 2011 17:25
Cálculo: Limites, Derivadas e Integrais
-
- Limite exponencial
por Jhennyfer » Qua Mai 14, 2014 20:07
- 5 Respostas
- 2842 Exibições
- Última mensagem por e8group

Sex Mai 16, 2014 13:09
Cálculo: Limites, Derivadas e Integrais
-
- [calculo] limite - exponencial
por beel » Dom Out 30, 2011 17:51
- 4 Respostas
- 2165 Exibições
- Última mensagem por LuizAquino

Dom Out 30, 2011 19:02
Cálculo: Limites, Derivadas e Integrais
-
- limite envolvendo exponencial
por renat » Dom Jun 11, 2017 20:37
- 0 Respostas
- 2838 Exibições
- Última mensagem por renat

Dom Jun 11, 2017 20:37
Cálculo: Limites, Derivadas e Integrais
-
- [LIMITES] Limite fundamental Exponencial
por antonelli2006 » Ter Set 20, 2011 05:54
- 1 Respostas
- 2036 Exibições
- Última mensagem por LuizAquino

Ter Set 20, 2011 12:22
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x\rightarrow+\infty}\left[{2}^{x}-{3}^{x} \right] \lim_{x\rightarrow+\infty}\left[{2}^{x}-{3}^{x} \right]](/latexrender/pictures/11a0c5ea6f36a9873525a8bd84161338.png)

 e
e 

![\lim_{x\rightarrow+\infty}\left[{2}^{x}-{3}^{x} \right] \lim_{x\rightarrow+\infty}\left[{2}^{x}-{3}^{x} \right]](/latexrender/pictures/11a0c5ea6f36a9873525a8bd84161338.png)

 e
e 

e
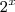 em evidência, note que:
em evidência, note que:
![= \lim_{x\to +\infty} 2^x\left[1 - \left(\frac{3}{2}\right)^x\right] = \lim_{x\to +\infty} 2^x\left[1 - \left(\frac{3}{2}\right)^x\right]](/latexrender/pictures/0f7698ee7b60a02862f70ffee6e929b5.png)



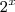 , note que:
, note que:






 .
.
 :
: