Sejam
 e
e  um ponto de acumulação de
um ponto de acumulação de  .
.a) Mostre que se ambos

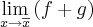 existem, então o
existem, então o  existe.
existe.b) Se

 , segue que
, segue que  existe?
existe?Ficarei agradecido se alguém souber resolver e puder me ajudar.
Até mais.

 e
e  um ponto de acumulação de
um ponto de acumulação de  .
.
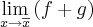 existem, então o
existem, então o  existe.
existe.
 , segue que
, segue que  existe?
existe?
Cleyson007 escreveu:Sejame
um ponto de acumulação de
.
a) Mostre que se ambose
existem, então o
existe.
 ;
; .
. exite
exite 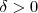 tal que
tal que  ;
; exite
exite 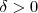 tal que
tal que  ;
; (com
(com  ), existe
), existe  tal que
tal que  .
. (com
(com  ), existe
), existe  tal que
tal que  .
. , temos que:
, temos que:




 existe e é igual a (M - L).
existe e é igual a (M - L).Cleyson007 escreveu:b) Se
, segue que
existe?
 . Note que
. Note que  e
e  existem, mas
existem, mas  não existe.
não existe.
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 12 visitantes