 por leds » Qua Abr 18, 2012 13:41
por leds » Qua Abr 18, 2012 13:41
A densidade de hebívoros tende a decrescer à medida que a distância da árvore mãe aumenta já que a densidade de comida decresce. Seja
x a distância em metros do tronco da ávore mãe. Os resultados de amostragem indicam que a densidade de semente no chão para
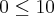
é dado por:
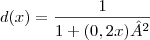
a e probabilidade de sobrevivência de não ser comido por hebívoros é:

Para q distância a razão é máxima?
-
leds
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qua Abr 18, 2012 13:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Biologia
- Andamento: cursando
 por LuizAquino » Qui Abr 19, 2012 11:52
por LuizAquino » Qui Abr 19, 2012 11:52
leds escreveu:A densidade de hebívoros tende a decrescer à medida que a distância da árvore mãe aumenta já que a densidade de comida decresce. Seja
x a distância em metros do tronco da ávore mãe. Os resultados de amostragem indicam que a densidade de semente no chão para
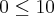
é dado por:
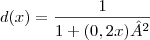
a e probabilidade de sobrevivência de não ser comido por hebívoros é:

Para q distância a razão é máxima?
Esse exercício é análogo ao que está nesse tópico:
viewtopic.php?f=120&t=7974Como aquele tópico é mais antigo e seu tópico é análogo a ele, o seu será removido para não haver duplicidade no fórum.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
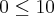 é dado por:
é dado por: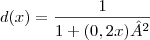


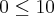 é dado por:
é dado por: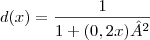


é dado por:



 , avisa que eu resolvo.
, avisa que eu resolvo.

