 por Priscilla Correa » Sáb Abr 07, 2012 15:44
por Priscilla Correa » Sáb Abr 07, 2012 15:44
![\lim_{x \rightarrow 0}\sqrt[n]x - \sqrt[n]p{}{} / x - p \lim_{x \rightarrow 0}\sqrt[n]x - \sqrt[n]p{}{} / x - p](/latexrender/pictures/a7f22620032ff7aceba3a45471e3768d.png)
Alguém pode me ajudar??
-
Priscilla Correa
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Sáb Abr 07, 2012 08:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: ENGENHARIA
- Andamento: cursando
 por LuizAquino » Sáb Abr 07, 2012 16:06
por LuizAquino » Sáb Abr 07, 2012 16:06
Priscilla Correa escreveu:![\lim_{x \rightarrow 0}\sqrt[n]x - \sqrt[n]p{}{} / x - p \lim_{x \rightarrow 0}\sqrt[n]x - \sqrt[n]p{}{} / x - p](/latexrender/pictures/a7f22620032ff7aceba3a45471e3768d.png)
Alguém pode me ajudar??
O que você escreveu é equivalente a:
![\lim_{x \to 0}\sqrt[n]{x} - \frac{\sqrt[n]{p}}{x} - p \lim_{x \to 0}\sqrt[n]{x} - \frac{\sqrt[n]{p}}{x} - p](/latexrender/pictures/92e91a908a724eb347af1b8da1846918.png)
Mas eu presumo que o exercício original seja:
![\lim_{x \to p}\frac{\sqrt[n]{x} - \sqrt[n]{p}}{x - p} \lim_{x \to p}\frac{\sqrt[n]{x} - \sqrt[n]{p}}{x - p}](/latexrender/pictures/7d25615a280b19a531a71b9386e8a584.png)
Se você queria dizer isso, então deveria ter escrito algo como:
![\lim_{x \to p}\left(\sqrt[n]{x} - \sqrt[n]{p}\right)/(x - p) \lim_{x \to p}\left(\sqrt[n]{x} - \sqrt[n]{p}\right)/(x - p)](/latexrender/pictures/cc844929dacec3a3f78b5b548166555e.png)
Note a importância do uso dos parênteses! Além disso, note que x tende a p e não a 0.
Falando agora sobre a resolução desse limite, note que:
![\lim_{x \to p}\frac{\sqrt[n]{x} - \sqrt[n]{p}}{x - p} = \lim_{x \to p} \frac{\sqrt[n]{x} - \sqrt[n]{p}}{\left(\sqrt[n]{x}\right)^n - \left(\sqrt[n]{p}\right)^n} \lim_{x \to p}\frac{\sqrt[n]{x} - \sqrt[n]{p}}{x - p} = \lim_{x \to p} \frac{\sqrt[n]{x} - \sqrt[n]{p}}{\left(\sqrt[n]{x}\right)^n - \left(\sqrt[n]{p}\right)^n}](/latexrender/pictures/b4a589302a6689d509ca436dfb2a3a3e.png)
Agora use o produto notável:
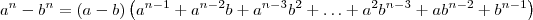
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Priscilla Correa » Sáb Abr 07, 2012 16:15
por Priscilla Correa » Sáb Abr 07, 2012 16:15
Obrigada pela resposta, eu fiquei meio confusa na hora de escrever a função e acabei digitando errado.
Então, eu resolvi e deu 1/0 (um sobre zero). Será que é isso mesmo???
-
Priscilla Correa
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Sáb Abr 07, 2012 08:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: ENGENHARIA
- Andamento: cursando
 por LuizAquino » Sáb Abr 07, 2012 16:19
por LuizAquino » Sáb Abr 07, 2012 16:19
Priscilla Correa escreveu:Obrigada pela resposta, eu fiquei meio confusa na hora de escrever a função e acabei digitando errado.
Então, eu resolvi e deu 1/0 (um sobre zero). Será que é isso mesmo???
O resultado não é esse. Envie a sua resolução para que possamos corrigi-la.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Priscilla Correa » Sáb Abr 07, 2012 16:33
por Priscilla Correa » Sáb Abr 07, 2012 16:33
Eu refiz e cheguei a outro resultado.
![\lim_{x \rightarrow p}(\sqrt[n]x - \sqrt[n]p{}{}) / (x - p)
= \lim_{x \rightarrow p}(\sqrt[n]x - \sqrt[n]p{}{})(\sqrt[n]x + \sqrt[n]p{}{})/ (x - p)(\sqrt[n]x + \sqrt[n]p{}{})= \lim_{x \rightarrow p} 1/(\sqrt[n]x + \sqrt[n]p{}{}) = 1/(\sqrt[n]p + \sqrt[n]p{}{}) \lim_{x \rightarrow p}(\sqrt[n]x - \sqrt[n]p{}{}) / (x - p)
= \lim_{x \rightarrow p}(\sqrt[n]x - \sqrt[n]p{}{})(\sqrt[n]x + \sqrt[n]p{}{})/ (x - p)(\sqrt[n]x + \sqrt[n]p{}{})= \lim_{x \rightarrow p} 1/(\sqrt[n]x + \sqrt[n]p{}{}) = 1/(\sqrt[n]p + \sqrt[n]p{}{})](/latexrender/pictures/424b363154efd31ac8399945d56983f2.png)
Será que está certo??
-
Priscilla Correa
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Sáb Abr 07, 2012 08:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: ENGENHARIA
- Andamento: cursando
 por LuizAquino » Sáb Abr 07, 2012 16:54
por LuizAquino » Sáb Abr 07, 2012 16:54
Priscilla Correa escreveu:Eu refiz e cheguei a outro resultado.
![\lim_{x \rightarrow p}(\sqrt[n]x - \sqrt[n]p{}{}) / (x - p)
= \lim_{x \rightarrow p}(\sqrt[n]x - \sqrt[n]p{}{})(\sqrt[n]x + \sqrt[n]p{}{})/ (x - p)(\sqrt[n]x + \sqrt[n]p{}{})= \lim_{x \rightarrow p} 1/(\sqrt[n]x + \sqrt[n]p{}{}) = 1/(\sqrt[n]p + \sqrt[n]p{}{}) \lim_{x \rightarrow p}(\sqrt[n]x - \sqrt[n]p{}{}) / (x - p)
= \lim_{x \rightarrow p}(\sqrt[n]x - \sqrt[n]p{}{})(\sqrt[n]x + \sqrt[n]p{}{})/ (x - p)(\sqrt[n]x + \sqrt[n]p{}{})= \lim_{x \rightarrow p} 1/(\sqrt[n]x + \sqrt[n]p{}{}) = 1/(\sqrt[n]p + \sqrt[n]p{}{})](/latexrender/pictures/424b363154efd31ac8399945d56983f2.png)
Será que está certo??
Está errado. O seu erro está em achar que
![\left(\sqrt[n]{x} - \sqrt[n]{p}\right)\right\left(\sqrt[n]{x} + \sqrt[n]{p}\right) \left(\sqrt[n]{x} - \sqrt[n]{p}\right)\right\left(\sqrt[n]{x} + \sqrt[n]{p}\right)](/latexrender/pictures/9b2492a0192f29c4465c28e77cea554a.png)
é igual a x - p.
Por exemplo, note que:
![\left(\sqrt[3]{x} - \sqrt[3]{p}\right)\right\left(\sqrt[3]{x} + \sqrt[3]{p}\right) = \left(\sqrt[3]{x}\right)^2 - \left(\sqrt[3]{p}\right)^2 \neq x - p \left(\sqrt[3]{x} - \sqrt[3]{p}\right)\right\left(\sqrt[3]{x} + \sqrt[3]{p}\right) = \left(\sqrt[3]{x}\right)^2 - \left(\sqrt[3]{p}\right)^2 \neq x - p](/latexrender/pictures/661d5ced03d4a6f842f7ddeee08aa636.png)
Usando o produto notável que indiquei anteriormente, temos que:
![\lim_{x \to p}\frac{\sqrt[n]{x} - \sqrt[n]{p}}{x - p} = \lim_{x \to p} \frac{\sqrt[n]{x} - \sqrt[n]{p}}{\left(\sqrt[n]{x}\right)^n - \left(\sqrt[n]{p}\right)^n} \lim_{x \to p}\frac{\sqrt[n]{x} - \sqrt[n]{p}}{x - p} = \lim_{x \to p} \frac{\sqrt[n]{x} - \sqrt[n]{p}}{\left(\sqrt[n]{x}\right)^n - \left(\sqrt[n]{p}\right)^n}](/latexrender/pictures/b4a589302a6689d509ca436dfb2a3a3e.png)
![= \lim_{x\to p}\frac{\sqrt[n]{x} - \sqrt[n]{p}}{(\sqrt[n]{x} - \sqrt[n]{p})(\sqrt[n]{x}^{n-1} + \sqrt[n]{x}^{n-2}\sqrt[n]{p} + \sqrt[n]{x}^{n-3}\sqrt[n]{p}^2+\ldots \sqrt[n]{x}^2\sqrt[n]{p}^{n-3} + \sqrt[n]{x}\sqrt[n]{p}^{n-2} + \sqrt[n]{p}^{n-1})} = \lim_{x\to p}\frac{\sqrt[n]{x} - \sqrt[n]{p}}{(\sqrt[n]{x} - \sqrt[n]{p})(\sqrt[n]{x}^{n-1} + \sqrt[n]{x}^{n-2}\sqrt[n]{p} + \sqrt[n]{x}^{n-3}\sqrt[n]{p}^2+\ldots \sqrt[n]{x}^2\sqrt[n]{p}^{n-3} + \sqrt[n]{x}\sqrt[n]{p}^{n-2} + \sqrt[n]{p}^{n-1})}](/latexrender/pictures/c19e8794a432ec461382d19217519ac7.png)
![= \lim_{x\to p}\frac{1}{\sqrt[n]{x}^{n-1} + \sqrt[n]{x}^{n-2}\sqrt[n]{p} + \sqrt[n]{x}^{n-3}\sqrt[n]{p}^2+\ldots \sqrt[n]{x}^2\sqrt[n]{p}^{n-3} + \sqrt[n]{x}\sqrt[n]{p}^{n-2} + \sqrt[n]{p}^{n-1}} = \lim_{x\to p}\frac{1}{\sqrt[n]{x}^{n-1} + \sqrt[n]{x}^{n-2}\sqrt[n]{p} + \sqrt[n]{x}^{n-3}\sqrt[n]{p}^2+\ldots \sqrt[n]{x}^2\sqrt[n]{p}^{n-3} + \sqrt[n]{x}\sqrt[n]{p}^{n-2} + \sqrt[n]{p}^{n-1}}](/latexrender/pictures/ec764a5d42aa7595b872abd5c8c65756.png)
Agora tente terminar o exercício.
Uma dica: para que você possa entender melhor o que acontece no caso geral, estude o que acontece em um caso particular. Por exemplo, quando n = 3 temos que:
![\lim_{x \to p}\frac{\sqrt[3]{x} - \sqrt[3]{p}}{x - p} = \lim_{x \to p} \frac{\sqrt[3]{x} - \sqrt[3]{p}}{\left(\sqrt[3]{x}\right)^3 - \left(\sqrt[3]{p}\right)^3} \lim_{x \to p}\frac{\sqrt[3]{x} - \sqrt[3]{p}}{x - p} = \lim_{x \to p} \frac{\sqrt[3]{x} - \sqrt[3]{p}}{\left(\sqrt[3]{x}\right)^3 - \left(\sqrt[3]{p}\right)^3}](/latexrender/pictures/920673a53c1c1a2ff76565584347eda7.png)
![= \lim_{x\to p}\frac{\sqrt[3]{x} - \sqrt[3]{p}}{\left(\sqrt[3]{x} - \sqrt[3]{p}\right)\left(\sqrt[3]{x}^{2} + \sqrt[3]{x}\sqrt[3]{p} + \sqrt[3]{p}^2\right)} = \lim_{x\to p}\frac{\sqrt[3]{x} - \sqrt[3]{p}}{\left(\sqrt[3]{x} - \sqrt[3]{p}\right)\left(\sqrt[3]{x}^{2} + \sqrt[3]{x}\sqrt[3]{p} + \sqrt[3]{p}^2\right)}](/latexrender/pictures/ab2a22f401583e947560e206556b18bd.png)
![= \lim_{x\to p}\frac{1}{\sqrt[3]{x}^{2} + \sqrt[3]{x}\sqrt[3]{p} + \sqrt[3]{p}^2} = \lim_{x\to p}\frac{1}{\sqrt[3]{x}^{2} + \sqrt[3]{x}\sqrt[3]{p} + \sqrt[3]{p}^2}](/latexrender/pictures/dc482690dafb549a9993a5342708e544.png)
Agora tente continuar.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] Gráfico e limite para função maior inteiro
 por Raphaela_sf » Qui Abr 05, 2012 19:26
por Raphaela_sf » Qui Abr 05, 2012 19:26
- 1 Respostas
- 6650 Exibições
- Última mensagem por LuizAquino

Qui Abr 05, 2012 20:53
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções reais de várias variáveis
por Bianca_R » Dom Nov 04, 2012 17:17
- 1 Respostas
- 4796 Exibições
- Última mensagem por MarceloFantini

Dom Nov 04, 2012 19:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite trigonométrico] Como calculo este limite?
por Ronaldobb » Qua Nov 07, 2012 23:14
- 3 Respostas
- 5127 Exibições
- Última mensagem por Ronaldobb

Qui Nov 08, 2012 07:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] limite trigonométrico quando x tende ao infinito
por Ge_dutra » Seg Jan 28, 2013 10:13
- 2 Respostas
- 7270 Exibições
- Última mensagem por Ge_dutra

Ter Jan 29, 2013 14:20
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções piso (maior inteiro)
por ViniciusAlmeida » Sáb Fev 14, 2015 10:09
- 2 Respostas
- 4446 Exibições
- Última mensagem por adauto martins

Qui Fev 19, 2015 15:01
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x \rightarrow 0}\sqrt[n]x - \sqrt[n]p{}{} / x - p \lim_{x \rightarrow 0}\sqrt[n]x - \sqrt[n]p{}{} / x - p](/latexrender/pictures/a7f22620032ff7aceba3a45471e3768d.png)

![\lim_{x \rightarrow 0}\sqrt[n]x - \sqrt[n]p{}{} / x - p \lim_{x \rightarrow 0}\sqrt[n]x - \sqrt[n]p{}{} / x - p](/latexrender/pictures/a7f22620032ff7aceba3a45471e3768d.png)

![\lim_{x \to 0}\sqrt[n]{x} - \frac{\sqrt[n]{p}}{x} - p \lim_{x \to 0}\sqrt[n]{x} - \frac{\sqrt[n]{p}}{x} - p](/latexrender/pictures/92e91a908a724eb347af1b8da1846918.png)
![\lim_{x \to p}\frac{\sqrt[n]{x} - \sqrt[n]{p}}{x - p} \lim_{x \to p}\frac{\sqrt[n]{x} - \sqrt[n]{p}}{x - p}](/latexrender/pictures/7d25615a280b19a531a71b9386e8a584.png)
![\lim_{x \to p}\left(\sqrt[n]{x} - \sqrt[n]{p}\right)/(x - p) \lim_{x \to p}\left(\sqrt[n]{x} - \sqrt[n]{p}\right)/(x - p)](/latexrender/pictures/cc844929dacec3a3f78b5b548166555e.png)
![\lim_{x \to p}\frac{\sqrt[n]{x} - \sqrt[n]{p}}{x - p} = \lim_{x \to p} \frac{\sqrt[n]{x} - \sqrt[n]{p}}{\left(\sqrt[n]{x}\right)^n - \left(\sqrt[n]{p}\right)^n} \lim_{x \to p}\frac{\sqrt[n]{x} - \sqrt[n]{p}}{x - p} = \lim_{x \to p} \frac{\sqrt[n]{x} - \sqrt[n]{p}}{\left(\sqrt[n]{x}\right)^n - \left(\sqrt[n]{p}\right)^n}](/latexrender/pictures/b4a589302a6689d509ca436dfb2a3a3e.png)
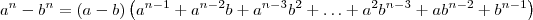



![\lim_{x \rightarrow p}(\sqrt[n]x - \sqrt[n]p{}{}) / (x - p)
= \lim_{x \rightarrow p}(\sqrt[n]x - \sqrt[n]p{}{})(\sqrt[n]x + \sqrt[n]p{}{})/ (x - p)(\sqrt[n]x + \sqrt[n]p{}{})= \lim_{x \rightarrow p} 1/(\sqrt[n]x + \sqrt[n]p{}{}) = 1/(\sqrt[n]p + \sqrt[n]p{}{}) \lim_{x \rightarrow p}(\sqrt[n]x - \sqrt[n]p{}{}) / (x - p)
= \lim_{x \rightarrow p}(\sqrt[n]x - \sqrt[n]p{}{})(\sqrt[n]x + \sqrt[n]p{}{})/ (x - p)(\sqrt[n]x + \sqrt[n]p{}{})= \lim_{x \rightarrow p} 1/(\sqrt[n]x + \sqrt[n]p{}{}) = 1/(\sqrt[n]p + \sqrt[n]p{}{})](/latexrender/pictures/424b363154efd31ac8399945d56983f2.png)

![\left(\sqrt[n]{x} - \sqrt[n]{p}\right)\right\left(\sqrt[n]{x} + \sqrt[n]{p}\right) \left(\sqrt[n]{x} - \sqrt[n]{p}\right)\right\left(\sqrt[n]{x} + \sqrt[n]{p}\right)](/latexrender/pictures/9b2492a0192f29c4465c28e77cea554a.png) é igual a x - p.
é igual a x - p.![\left(\sqrt[3]{x} - \sqrt[3]{p}\right)\right\left(\sqrt[3]{x} + \sqrt[3]{p}\right) = \left(\sqrt[3]{x}\right)^2 - \left(\sqrt[3]{p}\right)^2 \neq x - p \left(\sqrt[3]{x} - \sqrt[3]{p}\right)\right\left(\sqrt[3]{x} + \sqrt[3]{p}\right) = \left(\sqrt[3]{x}\right)^2 - \left(\sqrt[3]{p}\right)^2 \neq x - p](/latexrender/pictures/661d5ced03d4a6f842f7ddeee08aa636.png)
![\lim_{x \to p}\frac{\sqrt[n]{x} - \sqrt[n]{p}}{x - p} = \lim_{x \to p} \frac{\sqrt[n]{x} - \sqrt[n]{p}}{\left(\sqrt[n]{x}\right)^n - \left(\sqrt[n]{p}\right)^n} \lim_{x \to p}\frac{\sqrt[n]{x} - \sqrt[n]{p}}{x - p} = \lim_{x \to p} \frac{\sqrt[n]{x} - \sqrt[n]{p}}{\left(\sqrt[n]{x}\right)^n - \left(\sqrt[n]{p}\right)^n}](/latexrender/pictures/b4a589302a6689d509ca436dfb2a3a3e.png)
![= \lim_{x\to p}\frac{\sqrt[n]{x} - \sqrt[n]{p}}{(\sqrt[n]{x} - \sqrt[n]{p})(\sqrt[n]{x}^{n-1} + \sqrt[n]{x}^{n-2}\sqrt[n]{p} + \sqrt[n]{x}^{n-3}\sqrt[n]{p}^2+\ldots \sqrt[n]{x}^2\sqrt[n]{p}^{n-3} + \sqrt[n]{x}\sqrt[n]{p}^{n-2} + \sqrt[n]{p}^{n-1})} = \lim_{x\to p}\frac{\sqrt[n]{x} - \sqrt[n]{p}}{(\sqrt[n]{x} - \sqrt[n]{p})(\sqrt[n]{x}^{n-1} + \sqrt[n]{x}^{n-2}\sqrt[n]{p} + \sqrt[n]{x}^{n-3}\sqrt[n]{p}^2+\ldots \sqrt[n]{x}^2\sqrt[n]{p}^{n-3} + \sqrt[n]{x}\sqrt[n]{p}^{n-2} + \sqrt[n]{p}^{n-1})}](/latexrender/pictures/c19e8794a432ec461382d19217519ac7.png)
![= \lim_{x\to p}\frac{1}{\sqrt[n]{x}^{n-1} + \sqrt[n]{x}^{n-2}\sqrt[n]{p} + \sqrt[n]{x}^{n-3}\sqrt[n]{p}^2+\ldots \sqrt[n]{x}^2\sqrt[n]{p}^{n-3} + \sqrt[n]{x}\sqrt[n]{p}^{n-2} + \sqrt[n]{p}^{n-1}} = \lim_{x\to p}\frac{1}{\sqrt[n]{x}^{n-1} + \sqrt[n]{x}^{n-2}\sqrt[n]{p} + \sqrt[n]{x}^{n-3}\sqrt[n]{p}^2+\ldots \sqrt[n]{x}^2\sqrt[n]{p}^{n-3} + \sqrt[n]{x}\sqrt[n]{p}^{n-2} + \sqrt[n]{p}^{n-1}}](/latexrender/pictures/ec764a5d42aa7595b872abd5c8c65756.png)
![\lim_{x \to p}\frac{\sqrt[3]{x} - \sqrt[3]{p}}{x - p} = \lim_{x \to p} \frac{\sqrt[3]{x} - \sqrt[3]{p}}{\left(\sqrt[3]{x}\right)^3 - \left(\sqrt[3]{p}\right)^3} \lim_{x \to p}\frac{\sqrt[3]{x} - \sqrt[3]{p}}{x - p} = \lim_{x \to p} \frac{\sqrt[3]{x} - \sqrt[3]{p}}{\left(\sqrt[3]{x}\right)^3 - \left(\sqrt[3]{p}\right)^3}](/latexrender/pictures/920673a53c1c1a2ff76565584347eda7.png)
![= \lim_{x\to p}\frac{\sqrt[3]{x} - \sqrt[3]{p}}{\left(\sqrt[3]{x} - \sqrt[3]{p}\right)\left(\sqrt[3]{x}^{2} + \sqrt[3]{x}\sqrt[3]{p} + \sqrt[3]{p}^2\right)} = \lim_{x\to p}\frac{\sqrt[3]{x} - \sqrt[3]{p}}{\left(\sqrt[3]{x} - \sqrt[3]{p}\right)\left(\sqrt[3]{x}^{2} + \sqrt[3]{x}\sqrt[3]{p} + \sqrt[3]{p}^2\right)}](/latexrender/pictures/ab2a22f401583e947560e206556b18bd.png)
![= \lim_{x\to p}\frac{1}{\sqrt[3]{x}^{2} + \sqrt[3]{x}\sqrt[3]{p} + \sqrt[3]{p}^2} = \lim_{x\to p}\frac{1}{\sqrt[3]{x}^{2} + \sqrt[3]{x}\sqrt[3]{p} + \sqrt[3]{p}^2}](/latexrender/pictures/dc482690dafb549a9993a5342708e544.png)



 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.