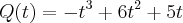 expressa a quantidade de peças produzidas por um operário em t horas, numa fabrica. Determine:
expressa a quantidade de peças produzidas por um operário em t horas, numa fabrica. Determine:a) a função que da a produção instantânea.
R- "achei" (me disseram) que a resposta é a derivada (
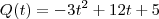 ), contudo, gostaria de uma explicação de porque a simples derivação nos leva a achar produção instantânea?
), contudo, gostaria de uma explicação de porque a simples derivação nos leva a achar produção instantânea?b) para calcular a quantidade de peças produzidas em 2 horas devo simplesmente proceder a resolução da equação? Assim a resposta é:
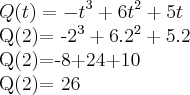
c)Como faço para achar a quantidade Máxima de peças que o operário produz?
Desde já agradeço.


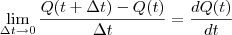 . Ou seja, você pega variações da quantidade de produtos e divide pela variação do tempo. Quando esta variação é muito pequena, ou infinitesimal, diremos que é a derivada.
. Ou seja, você pega variações da quantidade de produtos e divide pela variação do tempo. Quando esta variação é muito pequena, ou infinitesimal, diremos que é a derivada. 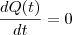 .
.

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.