 por lendersonfisica » Sex Fev 24, 2012 17:32
por lendersonfisica » Sex Fev 24, 2012 17:32
]Olá. Boa tarde. Gostaria que alguem me ajuda-se a desenvolver uma explicação bem detalhada da questão a seguir, utilizando as coordenadas polares para analisar a existência do limite no ponto (0,0);
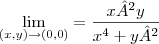
Obrigado Estou aguardando respostas. E tambem tentando desenvolver a questão.
Desde já Grato.
By: Lenderson Francisco Pedro José Souza da Silva
-
lendersonfisica
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Fev 24, 2012 17:04
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física
- Andamento: cursando
 por LuizAquino » Sáb Fev 25, 2012 20:02
por LuizAquino » Sáb Fev 25, 2012 20:02
lendersonfisica escreveu:Gostaria que alguem me ajuda-se a desenvolver uma explicação bem detalhada da questão a seguir, utilizando as coordenadas polares para analisar a existência do limite no ponto (0,0);
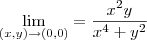
Eu presumo que o limite seja:
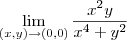
Note que você escreveu o símbolo "=" em um local inadequado.
Como você já deve ter feito, primeiro você precisa transferir esse limite para as coordenadas polares. Para isso, basta utilizar
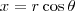
,
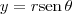
e fazer r tender para 0.
Temos então que:
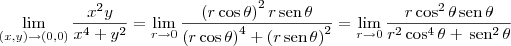
Agora basta escolher dois caminhos para os quais o limite seja distinto.
Escolha por exemplo o caminho tal que os pontos se aproximam de (0, 0) pela reta polar

.
Em seguida, escolha o caminho tal que os pontos se aproximam de (0, 0) pela espiral

.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por lendersonfisica » Dom Fev 26, 2012 11:05
por lendersonfisica » Dom Fev 26, 2012 11:05
Presumio Corretamente amigo!
Muito obrigado foi de muita ajuda, para intender uma questão que me foi passada para explicar na aula.
-
lendersonfisica
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Fev 24, 2012 17:04
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Vetores ! Por favor, da forma mais detalhada possível.Grato
por johnatta » Sáb Mai 23, 2015 11:08
- 0 Respostas
- 0 Exibições
- Última mensagem por Visitante

Qua Dez 31, 1969 22:00
Geometria Analítica
-
- Vetores ! Por favor, da forma mais detalhada possível.Grato
por johnatta » Sáb Mai 23, 2015 12:45
- 0 Respostas
- 1130 Exibições
- Última mensagem por johnatta

Sáb Mai 23, 2015 12:45
Geometria Analítica
-
- Limite Continuidade
por Claudin » Sáb Out 01, 2011 11:33
- 10 Respostas
- 5810 Exibições
- Última mensagem por Claudin

Seg Out 03, 2011 10:37
Cálculo: Limites, Derivadas e Integrais
-
- Continuidade Limite
por CaioLemos » Qui Mar 22, 2012 13:18
- 2 Respostas
- 2021 Exibições
- Última mensagem por CaioLemos

Qui Mar 22, 2012 17:39
Cálculo: Limites, Derivadas e Integrais
-
- Limite e Continuidade
por Thyago Quimica » Seg Mai 21, 2012 14:11
- 1 Respostas
- 1669 Exibições
- Última mensagem por LuizAquino

Ter Mai 22, 2012 19:22
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
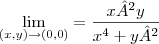

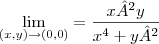

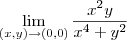
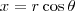 ,
, 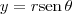 e fazer r tender para 0.
e fazer r tender para 0.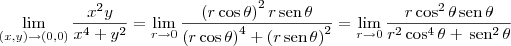
 .
. .
.

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.