 por joserd » Qua Jan 25, 2012 21:17
por joserd » Qua Jan 25, 2012 21:17
Seja R a região delimitada pelos gráficos de x=y^2 e x=9. Determine o volume do sólido S que tem R como base , e tal que toda seção transversal por um plano perpendicular ao eixo Ox seja um triangulo equilátero. Esboce o sólido.
Consegui apenas encontrar os pontos comuns e fazer os gráficos da área . Não tenho ideia de como clacular o volume e do esboço do sólido.
-
joserd
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Sex Set 16, 2011 20:57
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: analise
- Andamento: formado
 por LuizAquino » Qui Jan 26, 2012 00:32
por LuizAquino » Qui Jan 26, 2012 00:32
joserd escreveu:Seja R a região delimitada pelos gráficos de x=y^2 e x=9. Determine o volume do sólido S que tem R como base , e tal que toda seção transversal por um plano perpendicular ao eixo Ox seja um triangulo equilátero. Esboce o sólido.
joserd escreveu:Consegui apenas encontrar os pontos comuns e fazer os gráficos da área . Não tenho ideia de como clacular o volume e do esboço do sólido.
As figuras abaixo ilustram a região R e o sólido S.
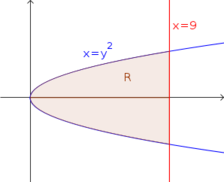
- região_R.png (10.17 KiB) Exibido 809 vezes
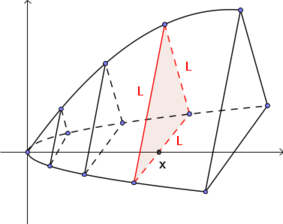
- sólido_S.png (33.16 KiB) Exibido 809 vezes
Para determinar o volume de S, comece determinando a área A do triângulo equilátero destacado em função da posição x.
Para isso, note que
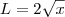
.
Desse modo, temos que a área A é dada por:
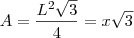
Enxergando a área A como uma função de x, temos que o volume V de S será dado por:
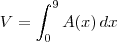
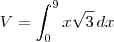
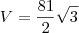
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Volume do Solido
por leha » Qui Dez 10, 2009 10:22
- 3 Respostas
- 3399 Exibições
- Última mensagem por leha

Seg Dez 14, 2009 13:44
Cálculo: Limites, Derivadas e Integrais
-
- Volume de sólido
 por Manoella » Seg Fev 21, 2011 23:41
por Manoella » Seg Fev 21, 2011 23:41
- 1 Respostas
- 2474 Exibições
- Última mensagem por LuizAquino

Ter Fev 22, 2011 11:38
Cálculo: Limites, Derivadas e Integrais
-
- volume de um sólido
 por Andreza » Seg Nov 14, 2011 14:26
por Andreza » Seg Nov 14, 2011 14:26
- 7 Respostas
- 8559 Exibições
- Última mensagem por Andreza

Sex Nov 25, 2011 10:05
Geometria Espacial
-
- volume de um sólido
por Priscila_moraes » Dom Dez 04, 2011 18:55
- 2 Respostas
- 2734 Exibições
- Última mensagem por LuizAquino

Dom Dez 04, 2011 19:56
Cálculo: Limites, Derivadas e Integrais
-
- volume de um sólido
por ah001334 » Ter Dez 20, 2011 10:47
- 1 Respostas
- 1840 Exibições
- Última mensagem por LuizAquino

Ter Dez 20, 2011 11:24
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


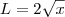 .
.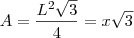
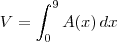
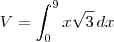
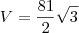

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
