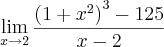
No resultado apresenta f(x)=
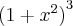 e a derivada ( f '(2) = 300 ). Gostaria de saber como foi possivel obter esses resultados. passo a passo.
e a derivada ( f '(2) = 300 ). Gostaria de saber como foi possivel obter esses resultados. passo a passo.obrigado

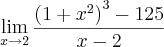
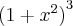 e a derivada ( f '(2) = 300 ). Gostaria de saber como foi possivel obter esses resultados. passo a passo.
e a derivada ( f '(2) = 300 ). Gostaria de saber como foi possivel obter esses resultados. passo a passo.
giboia90 escreveu:Expresse o limite abaixo como uma derivada, e então calcule o limite.
giboia90 escreveu:No resultado apresentae a derivada ( f'(2) = 300 ). Gostaria de saber como foi possivel obter esses resultados. passo a passo.
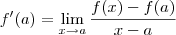
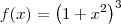 .
.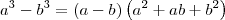 .
.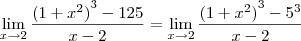
![= \lim_{x\to 2}\frac{\left(x^2 - 4\right)\left[\left(1+x^2\right)^2 + 5\left(1+x^2\right) + 25\right]}{x-2} = \lim_{x\to 2}\frac{\left(x^2 - 4\right)\left[\left(1+x^2\right)^2 + 5\left(1+x^2\right) + 25\right]}{x-2}](/latexrender/pictures/4aca0abd9bc1ae6a867a555db1d48290.png)
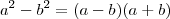 .
.

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)