 por matmatco » Qua Nov 30, 2011 13:47
por matmatco » Qua Nov 30, 2011 13:47
olá,
estou com um problema nesse limite
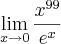
...não estou conseguindo fazer os proximos passos , sei que o limite da zero.
obrigado
-
matmatco
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qua Ago 24, 2011 17:32
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica UFV
- Andamento: cursando
 por LuizAquino » Qua Nov 30, 2011 17:06
por LuizAquino » Qua Nov 30, 2011 17:06
matmatco escreveu:estou com um problema nesse limite
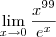
...não estou conseguindo fazer os proximos passos , sei que o limite da zero.
Como não há indeterminação, a solução é direta:
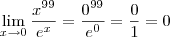
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por matmatco » Qua Nov 30, 2011 17:31
por matmatco » Qua Nov 30, 2011 17:31
me desculpe eu cometi um erro x nao esta tendendo a zero e sim a infinito
-
matmatco
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qua Ago 24, 2011 17:32
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica UFV
- Andamento: cursando
 por MarceloFantini » Qua Nov 30, 2011 22:15
por MarceloFantini » Qua Nov 30, 2011 22:15
Você aplicou a regra de L'Hopital?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por LuizAquino » Sex Dez 02, 2011 16:53
por LuizAquino » Sex Dez 02, 2011 16:53
matmatco escreveu:me desculpe eu cometi um erro x nao esta tendendo a zero e sim a infinito
Então você deseja calcular o limite:
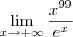
Basta aplicar 99 vezes a regra de L'Hospital.
Para isso, aqui vão duas dicas:
(i)
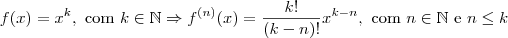
;
(ii)
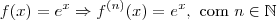
.
ObservaçãoLembre-se que a notação
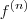
representa a n-ésima derivada de
f.
Por exemplo, temos que
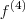
denota a quarta derivada de
f .
Editado pela última vez por
LuizAquino em Sáb Dez 03, 2011 11:20, em um total de 1 vez.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por matmatco » Sáb Dez 03, 2011 07:10
por matmatco » Sáb Dez 03, 2011 07:10
obrigado.
-
matmatco
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qua Ago 24, 2011 17:32
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica UFV
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Regra de L'Hospital
por Claudin » Qui Jul 14, 2011 20:26
- 2 Respostas
- 1924 Exibições
- Última mensagem por Claudin

Qui Jul 14, 2011 20:46
Cálculo: Limites, Derivadas e Integrais
-
- Regra de L'Hospital
por Claudin » Qui Jul 14, 2011 21:16
- 9 Respostas
- 3358 Exibições
- Última mensagem por MarceloFantini

Sáb Jul 16, 2011 15:20
Cálculo: Limites, Derivadas e Integrais
-
- Regra de L'hospital
 por samra » Dom Ago 19, 2012 18:37
por samra » Dom Ago 19, 2012 18:37
- 1 Respostas
- 2437 Exibições
- Última mensagem por e8group

Dom Ago 19, 2012 19:58
Cálculo: Limites, Derivadas e Integrais
-
- Derivada regra de L'Hospital
por Wumaxeb » Sex Mai 27, 2011 22:19
- 2 Respostas
- 3114 Exibições
- Última mensagem por Molina

Sex Mai 27, 2011 23:24
Cálculo: Limites, Derivadas e Integrais
-
- [Regra de L'Hospital] Indeterminções
por erickm93 » Seg Jun 24, 2013 11:47
- 1 Respostas
- 1651 Exibições
- Última mensagem por Man Utd

Qui Jun 27, 2013 11:56
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
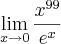 ...não estou conseguindo fazer os proximos passos , sei que o limite da zero.
...não estou conseguindo fazer os proximos passos , sei que o limite da zero.
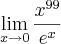 ...não estou conseguindo fazer os proximos passos , sei que o limite da zero.
...não estou conseguindo fazer os proximos passos , sei que o limite da zero.
...não estou conseguindo fazer os proximos passos , sei que o limite da zero.
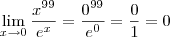



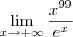
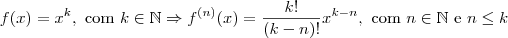 ;
;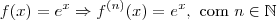 .
.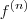 representa a n-ésima derivada de f.
representa a n-ésima derivada de f.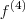 denota a quarta derivada de f .
denota a quarta derivada de f .


 .
.
 :
: