 por wildta » Seg Out 17, 2011 11:12
por wildta » Seg Out 17, 2011 11:12
Olá pessoal, to estudando limite e nao consegui fazer esse exercício.
Na verdade acho q to com dúvida quando se refere a raiz, provalmente tenho q revisar algumas matérias do ensimo médio...srrs
![\lim_{0} \frac{x}{\sqrt[2]{a+x}-\sqrt[2]{a}} \lim_{0} \frac{x}{\sqrt[2]{a+x}-\sqrt[2]{a}}](/latexrender/pictures/a3fe91daf310ea60e919b74958e68037.png)
Mais enfim, o professor disse q o resultado é
![2\sqrt[2]{a} 2\sqrt[2]{a}](/latexrender/pictures/1abb9fef0f03c17d762001a951df66a9.png)
Tem como vcs me ajudarem?
Obrigado.
-
wildta
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Out 17, 2011 00:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Sistemas de Informação
- Andamento: cursando
 por LuizAquino » Seg Out 17, 2011 12:15
por LuizAquino » Seg Out 17, 2011 12:15
wildta escreveu:Na verdade acho q to com dúvida quando se refere a raiz, provavelmente tenho q revisar algumas matérias do ensino médio...srrs
Sim, com certeza. Tentar aprender Cálculo "na marra" sem dominar os conteúdos do ensino fundamental e médio não costuma dar certo.
Vejamos agora o limite:
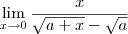
Multiplique o numerador e o denominador por
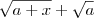
:

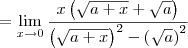
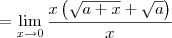
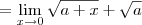
 Observação
ObservaçãoUm bom lugar para revisar os conteúdos do ensino fundamental é médio é o canal do Nerckie no YouTube:
http://www.youtube.com/nerckieSe você desejar acompanhar um curso de Cálculo I, então eu gostaria de recomendar o meu canal:
http://www.youtube.com/LCMAquino
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por wildta » Seg Out 17, 2011 13:59
por wildta » Seg Out 17, 2011 13:59
Valeuu cara..
-
wildta
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Out 17, 2011 00:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Sistemas de Informação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Limite indefinido com raiz quadrada.
por viniterranova » Qui Mar 28, 2013 22:29
- 1 Respostas
- 1527 Exibições
- Última mensagem por e8group

Sex Mar 29, 2013 00:48
Cálculo: Limites, Derivadas e Integrais
-
- [Raiz Cúbica e Raiz Quadrada] Muito difícil achar a solução.
por Leocondeuba » Sáb Mai 11, 2013 19:27
- 2 Respostas
- 7465 Exibições
- Última mensagem por Leocondeuba

Sáb Mai 11, 2013 20:42
Aritmética
-
- Raiz quadrada
por j1a4l0 » Qui Abr 22, 2010 18:05
- 5 Respostas
- 6008 Exibições
- Última mensagem por Neperiano

Sex Abr 23, 2010 09:35
Funções
-
- raiz quadrada
por jose henrique » Seg Ago 16, 2010 16:54
- 1 Respostas
- 2353 Exibições
- Última mensagem por MarceloFantini

Ter Ago 17, 2010 00:03
Álgebra Elementar
-
- [Raiz quadrada de 13] Na mão
por Mickdark » Dom Abr 08, 2012 20:00
- 4 Respostas
- 17651 Exibições
- Última mensagem por Mickdark

Qui Abr 12, 2012 09:56
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{0} \frac{x}{\sqrt[2]{a+x}-\sqrt[2]{a}} \lim_{0} \frac{x}{\sqrt[2]{a+x}-\sqrt[2]{a}}](/latexrender/pictures/a3fe91daf310ea60e919b74958e68037.png)
![2\sqrt[2]{a} 2\sqrt[2]{a}](/latexrender/pictures/1abb9fef0f03c17d762001a951df66a9.png)

![\lim_{0} \frac{x}{\sqrt[2]{a+x}-\sqrt[2]{a}} \lim_{0} \frac{x}{\sqrt[2]{a+x}-\sqrt[2]{a}}](/latexrender/pictures/a3fe91daf310ea60e919b74958e68037.png)
![2\sqrt[2]{a} 2\sqrt[2]{a}](/latexrender/pictures/1abb9fef0f03c17d762001a951df66a9.png)

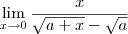
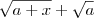 :
:
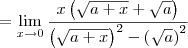
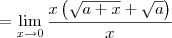
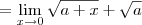



 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
