romulo39 escreveu:Prove usando o Método da Bissecção e o Teorema de Bolzano que 0,8832 é um valor aproximado, com 4 algarismos decimais exatos, da raiz positiva da equação
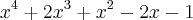
Considere a função
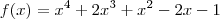
.
Note que
f é contínua, f(0) = -1 e f(1) = 1. Como f(0) < 0 < f(1), pelo Teorema de Bolzano existe um número
a no intervalo [0, 1] tal que
f(
a) = 0.
Vamos dividir o intervalo [0, 1] ao meio, ficando assim com os intervalos [0, 1/2] e [1/2, 1].
Temos que
f(1/2) = -23/16. Como
f(1/2) < 0 <
f(1), pelo Teorema de Bolzano existe um número
b no intervalo [1/2, 1] tal que
f(
b) = 0.
Vamos agora dividir o intervalo [1/2, 1] ao meio, ficando assim com os intervalos [1/2, 3/4] e [3/4, 1].
Temos que
f(3/4) = -199/256. Como
f(3/4) < 0 <
f(1), pelo Teorema de Bolzano existe um número
c no intervalo [3/4, 1] tal que
f(
c) = 0.
Agora continue o processo, dividindo o intervalo [3/4, 1] ao meio.
Você irá interromper o processo quando chegar no nível de aproximação desejado para a raiz.
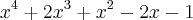

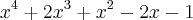

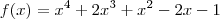 .
.