por Megatron32 » Ter Set 13, 2011 14:34
por Megatron32 » Ter Set 13, 2011 14:34
-
Megatron32
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Ter Set 13, 2011 14:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia mecanica
- Andamento: cursando
 por LuizAquino » Ter Set 13, 2011 18:12
por LuizAquino » Ter Set 13, 2011 18:12
Eu vou fazer uma delas e você tenta o restante.
Vamos considerar que y é função de x. Ou seja, podemos escrever que y = f(x).
Então a função implícita
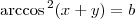
pode ser vista como

.
Note que temos uma composição de três funções. Por exemplo, considere que:
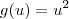
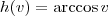
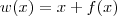
Com isso, a equação pode ser reescrita como g(h(w(x))) = b. Precisamos aplicar a regra da cadeia para calcular a derivada.
![[g(h(w(x)))]^\prime = b^\prime [g(h(w(x)))]^\prime = b^\prime](/latexrender/pictures/415114119bbf40f91d6cb918dcf6e461.png)
![g^\prime(h(w(x)))[h(w(x))]^\prime = 0 g^\prime(h(w(x)))[h(w(x))]^\prime = 0](/latexrender/pictures/5d08a00d13fc469d575e8906dfd68915.png)
![g^\prime(h(w(x)))h^\prime(w(x))[w(x)]^\prime = 0 g^\prime(h(w(x)))h^\prime(w(x))[w(x)]^\prime = 0](/latexrender/pictures/45b212da56bb746a35204f8974074c46.png)
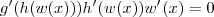
Calculando a derivada de cada função separadamente, sabemos que
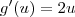
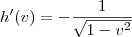
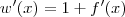
Agora, fazendo as substituições temos que:
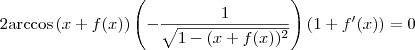
Lembrando que
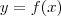
e
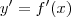
, ficamos com
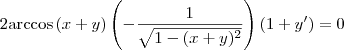 Observação
ObservaçãoSe você precisar revisar os conceitos de regra da cadeia e derivada de função implícita, então veja se as
vídeo-aulas "13. Cálculo I - Regra da Cadeia" e "14. Cálculo I - Derivada de Função Implícita" podem lhe ajudar.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Derivação implicita , quem ajuda ?
por Loretto » Ter Ago 03, 2010 02:15
- 4 Respostas
- 5124 Exibições
- Última mensagem por LuizAquino

Qua Mar 09, 2011 22:03
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Função Implicita
por fabriel » Sex Mar 15, 2013 13:27
- 1 Respostas
- 1539 Exibições
- Última mensagem por e8group

Sex Mar 15, 2013 21:50
Cálculo: Limites, Derivadas e Integrais
-
- Função implícita; Questão complicada!
por jemourafer » Qui Mai 17, 2012 18:30
- 4 Respostas
- 4254 Exibições
- Última mensagem por Fabio Wanderley

Sáb Mai 19, 2012 03:16
Cálculo: Limites, Derivadas e Integrais
-
- Função de uma variavel (cartesiana, paramétrica e implícita)
por rhmgh » Dom Ago 12, 2012 21:20
- 3 Respostas
- 1815 Exibições
- Última mensagem por MarceloFantini

Qua Ago 15, 2012 10:27
Funções
-
- [Derivada] Função Implicita-duvidas na resoluão.
por fabriel » Dom Mar 17, 2013 01:11
- 3 Respostas
- 2086 Exibições
- Última mensagem por e8group

Dom Mar 17, 2013 14:39
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
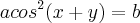
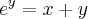
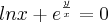


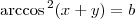 pode ser vista como
pode ser vista como  .
.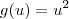
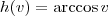
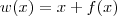
![[g(h(w(x)))]^\prime = b^\prime [g(h(w(x)))]^\prime = b^\prime](/latexrender/pictures/415114119bbf40f91d6cb918dcf6e461.png)
![g^\prime(h(w(x)))[h(w(x))]^\prime = 0 g^\prime(h(w(x)))[h(w(x))]^\prime = 0](/latexrender/pictures/5d08a00d13fc469d575e8906dfd68915.png)
![g^\prime(h(w(x)))h^\prime(w(x))[w(x)]^\prime = 0 g^\prime(h(w(x)))h^\prime(w(x))[w(x)]^\prime = 0](/latexrender/pictures/45b212da56bb746a35204f8974074c46.png)
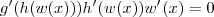
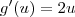
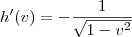
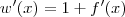
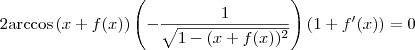
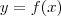 e
e 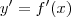 , ficamos com
, ficamos com