 por paula luna » Seg Ago 22, 2011 21:52
por paula luna » Seg Ago 22, 2011 21:52
-
paula luna
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Qui Mai 05, 2011 21:56
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por LuizAquino » Ter Ago 23, 2011 08:24
por LuizAquino » Ter Ago 23, 2011 08:24
Você fez a substituição
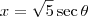
.
Desenvolvendo essa equação para aparecer o seno do ângulo, obtemos
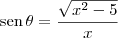
.
Você deve ter se atrapalhado nesse desenvolvimento. Envie a sua resolução dessa parte para que possamos identificar o problema.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por paula luna » Ter Ago 23, 2011 15:58
por paula luna » Ter Ago 23, 2011 15:58
Nossa! Claro! pura desatençao... mas é perdoavel,, trigonometria por vezes torna-se uma coisa extremamente tediosa com suas inumeras formas de simplificar ( ou de dificultar ). Toda hora que acho uma resposta, tenho que fazer varias simplificaçoes para dai entao saber se esta ou nao certa. Mas chega a ser um passatempo bem ... divertido , "Aprecie com moderaçao"

Obg todos que leram e ao Luiz que sempre responde nossas duvidas por mais "idiotas" que possam ser (parecer).
Obs.: Desculpa os erros de portugues, ha um motivo significante para escolher a area da eng. (nao que isso explique os erros

)
-
paula luna
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Qui Mai 05, 2011 21:56
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por LuizAquino » Ter Ago 23, 2011 19:11
por LuizAquino » Ter Ago 23, 2011 19:11
paula luna escreveu:Desculpa os erros de portugues, ha um motivo significante para escolher a area da eng. (nao que isso explique os erros

)
Com certeza o fato de escolhermos a área de exatas não é desculpa para descuidar do Português.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [calculo] calculo de integral - coordenada esferica
por fatalshootxd » Ter Mar 31, 2015 00:43
- 1 Respostas
- 4532 Exibições
- Última mensagem por adauto martins

Sáb Abr 04, 2015 16:13
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo Integral] Integral Definida
por ARCS » Sáb Fev 02, 2013 21:37
- 2 Respostas
- 3685 Exibições
- Última mensagem por e8group

Sáb Fev 02, 2013 22:13
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Cálculo de integral
por LAZAROTTI » Dom Set 30, 2012 19:52
- 0 Respostas
- 1197 Exibições
- Última mensagem por LAZAROTTI

Dom Set 30, 2012 19:52
Cálculo: Limites, Derivadas e Integrais
-
- cálculo de integral
por jmario » Ter Mai 18, 2010 12:25
- 1 Respostas
- 3277 Exibições
- Última mensagem por MarcosFreitas

Qua Jun 02, 2010 13:04
Cálculo: Limites, Derivadas e Integrais
-
- CALCULO DE INTEGRAL
por Jaison Werner » Sex Jan 07, 2011 18:58
- 4 Respostas
- 3173 Exibições
- Última mensagem por MarceloFantini

Sáb Jan 08, 2011 12:48
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\int_{}^{}\frac{dx}{{x}^{2}\sqrt[2]{{x}^{2}-5}} \int_{}^{}\frac{dx}{{x}^{2}\sqrt[2]{{x}^{2}-5}}](/latexrender/pictures/48ee08596de5cbcca42cb76e03f543a8.png)
![\sqrt[2]{{x}^{2}-5} = \sqrt[2]{5}.tg(\theta) \sqrt[2]{{x}^{2}-5} = \sqrt[2]{5}.tg(\theta)](/latexrender/pictures/96810cbb85747678feee797ea035b738.png)
![x = \sqrt[2]{5}.sec(\theta) x = \sqrt[2]{5}.sec(\theta)](/latexrender/pictures/8f8493f9b1418b2c23a1a2e8f6eda982.png)
![dx = \sqrt[2]{5}.sec(\theta).tg(\theta).d\theta dx = \sqrt[2]{5}.sec(\theta).tg(\theta).d\theta](/latexrender/pictures/a1bcc1436a25e2b7eb3a687b0db10d98.png)
![\int_{}^{}\frac{\sqrt[2]{5}.sec(\theta).tg(\theta).d\theta}{5.{sec}^{2}(\theta).\sqrt[2]{5}.tg(\theta)} \int_{}^{}\frac{\sqrt[2]{5}.sec(\theta).tg(\theta).d\theta}{5.{sec}^{2}(\theta).\sqrt[2]{5}.tg(\theta)}](/latexrender/pictures/a85c33ec8725dc819789c900fc86f421.png)

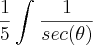

![\frac{1}{5}sen(\theta) = \frac{\sqrt[2]{{x}^{2}-5}}{5}+ C \frac{1}{5}sen(\theta) = \frac{\sqrt[2]{{x}^{2}-5}}{5}+ C](/latexrender/pictures/6fa255b9e28e5f709d80e5394c22a41b.png)
![\frac{\sqrt[2]{{x}^{2}-5}}{5x}+ C \frac{\sqrt[2]{{x}^{2}-5}}{5x}+ C](/latexrender/pictures/09a4f556903a3299fa9bd882b45e3f4f.png)





![\int_{}^{}\frac{dx}{{x}^{2}\sqrt[2]{{x}^{2}-5}} \int_{}^{}\frac{dx}{{x}^{2}\sqrt[2]{{x}^{2}-5}}](/latexrender/pictures/48ee08596de5cbcca42cb76e03f543a8.png)
![\sqrt[2]{{x}^{2}-5} = \sqrt[2]{5}.tg(\theta) \sqrt[2]{{x}^{2}-5} = \sqrt[2]{5}.tg(\theta)](/latexrender/pictures/96810cbb85747678feee797ea035b738.png)
![x = \sqrt[2]{5}.sec(\theta) x = \sqrt[2]{5}.sec(\theta)](/latexrender/pictures/8f8493f9b1418b2c23a1a2e8f6eda982.png)
![dx = \sqrt[2]{5}.sec(\theta).tg(\theta).d\theta dx = \sqrt[2]{5}.sec(\theta).tg(\theta).d\theta](/latexrender/pictures/a1bcc1436a25e2b7eb3a687b0db10d98.png)
![\int_{}^{}\frac{\sqrt[2]{5}.sec(\theta).tg(\theta).d\theta}{5.{sec}^{2}(\theta).\sqrt[2]{5}.tg(\theta)} \int_{}^{}\frac{\sqrt[2]{5}.sec(\theta).tg(\theta).d\theta}{5.{sec}^{2}(\theta).\sqrt[2]{5}.tg(\theta)}](/latexrender/pictures/a85c33ec8725dc819789c900fc86f421.png)

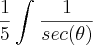

![\frac{1}{5}sen(\theta) = \frac{\sqrt[2]{{x}^{2}-5}}{5}+ C \frac{1}{5}sen(\theta) = \frac{\sqrt[2]{{x}^{2}-5}}{5}+ C](/latexrender/pictures/6fa255b9e28e5f709d80e5394c22a41b.png)
![\frac{\sqrt[2]{{x}^{2}-5}}{5x}+ C \frac{\sqrt[2]{{x}^{2}-5}}{5x}+ C](/latexrender/pictures/09a4f556903a3299fa9bd882b45e3f4f.png)





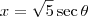 .
.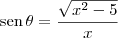 .
.

 )
)
)

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
