Sim... este é o valor de x no ponto mínimo de f(x)
Adicionei o gráfico das funções para vc observar isso...
Neste gráfico:
f é a parábola da função f(x)
f' é a reta inclinada dada pela derivada f'(x)
A é a interseção entre a reta da derivada e o eixo x
c é a reta perpendicular a x que passa pelo mesmo ponto A que a reta da derivada
B é o ponto de interseção entre a reta perpendicular c e a parábola f
Veja que o ponto B esta precisamente no vértice da função
Ou seja, a reta da derivada corta o eixo de x no ponto crítico da função..
como se trata de uma função de segundo grau, encontre o x vértice e verá que está certo...
Um abraço
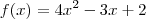
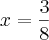 esse é o numero critico da função!!!
esse é o numero critico da função!!!
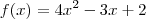
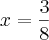 esse é o numero critico da função!!!
esse é o numero critico da função!!!

