Você deve estar referindo-se a limites do tipo:
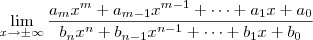
.
Nesses casos específicos, com
x assumindo valores positivos extremamente grandes ou valores negativos extremamento pequenos, no cálculo das somas que aparecem tanto no numerador quanto no denominador, os termos
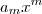
e
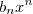
serão dominantes. Ou seja, os outros termos serão desprezíveis quando comparados com esses dois.
Nesse sentido, ao resolver limites como esses, há uma estratégia de reduzi-lo a:

.
Particularmente, eu não gosto de aplicar essa estratégia de redução. Eu acredito ser mais condizente dividir tanto o numerador quanto o denominador pelo monômio de maior grau e em seguida usar o fato que
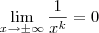
(com k natural e não nulo).
Por outro lado, em limites parecidos com esse, mas com
x aproximando-se de um número
c específico, cada termo que aparece nas somas é relevante. Por esse motivo não podemos efetuar a redução feita anteriormente. Ou seja, teremos que:

.


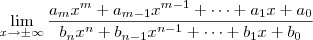 .
.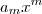 e
e 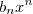 serão dominantes. Ou seja, os outros termos serão desprezíveis quando comparados com esses dois.
serão dominantes. Ou seja, os outros termos serão desprezíveis quando comparados com esses dois. .
.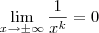 (com k natural e não nulo).
(com k natural e não nulo). .
.
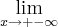 ?
? .
.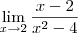 (resposta: 1/4).
(resposta: 1/4).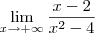 (resposta: 0).
(resposta: 0). .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
