 por liliduarte » Dom Mar 13, 2011 00:02
por liliduarte » Dom Mar 13, 2011 00:02
Boa noite gente. Minha professora passou um exercicio na faculdade e disse que após resolvido, se tirarmos a prova real, teria que dar 0. Eu resolvi o exercicio, tirei a prova, deu 0. Eu mostrei pra ela e ela disse que estava errado e me mostrou uma outra forma de resolver. Eu fiz do jeito dela e deu maior que 1, será que alguém pode me ajudar? O exercicio pede o valor de F1 e F2
- Anexos
-
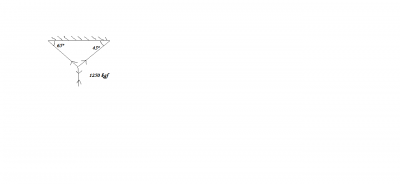
- Esse é o desenho do exercicio
-
liliduarte
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Mar 12, 2011 23:40
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Arquitetura e urbanismo
- Andamento: cursando
 por MarceloFantini » Dom Mar 13, 2011 03:27
por MarceloFantini » Dom Mar 13, 2011 03:27
Lili, poste a questão na íntegra. Com todo o respeito, seu desenho não faz muito sentido e faltam muitos dados.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por liliduarte » Dom Mar 13, 2011 13:26
por liliduarte » Dom Mar 13, 2011 13:26
O enunciado do exercicio é só esse: Determine os valores de F1 e F2. kgf= quilograma força.
Eu resolvi assim da primeira vez.
F1x= sen65º * F1
F2x= sen 45º * F2
F1y= cos 65º * F1
F2y= cos 45º * F2
-sen 65º * F1 - sen45º * F2=0
-0.90 * F1-0.70 * F2=0
-0.90 *F1= 0.70* F2
F1= 0.70 * F2/ 0.90
F1 = 0.77 F2
cos65º * F1 - cos 45 * F2 - 1250 = 0
cos 65º (0.77 F2) * cos45º * f2-1250=0
0.42 * (0.77 F2) -0.70 * F2-1250=0
0.32F2 - 0.70 * F2-1250=0
-0.38F2-1250=0
F2= -1250/-0.38
F2=3.28
como:
F1= -0.77 F2
F1= -0.77*3.28
F1= -2.52
prova real:
-sen 65* F1-sen45*F2=0
-0.90 * (-2.52) - 0.70 * 3.28= 0.02
Bom, é isso, espero que alguém possa me mostrar onde eu errei
-
liliduarte
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Mar 12, 2011 23:40
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Arquitetura e urbanismo
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Calculo]Alguém me ajuda nessa questão de calculo pfv.
por moeni » Seg Abr 04, 2022 21:54
- 0 Respostas
- 6498 Exibições
- Última mensagem por moeni

Seg Abr 04, 2022 21:54
Cálculo: Limites, Derivadas e Integrais
-
- [calculo] calculo de integral - coordenada esferica
por fatalshootxd » Ter Mar 31, 2015 00:43
- 1 Respostas
- 4532 Exibições
- Última mensagem por adauto martins

Sáb Abr 04, 2015 16:13
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo] Cálculo Polinômio Interpolador
 por barbara-rabello » Qui Out 22, 2015 20:07
por barbara-rabello » Qui Out 22, 2015 20:07
- 1 Respostas
- 2658 Exibições
- Última mensagem por adauto martins

Sáb Out 24, 2015 11:00
Cálculo: Limites, Derivadas e Integrais
-
- [Calculo] Exercícios de Calculo
por Thomas » Seg Mai 16, 2016 16:39
- 0 Respostas
- 0 Exibições
- Última mensagem por Visitante

Qua Dez 31, 1969 22:00
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo: Limites, Derivadas e Integrais] Cálculo de limites
por jeferson lopes » Ter Mar 26, 2013 08:49
- 2 Respostas
- 5569 Exibições
- Última mensagem por jeferson lopes

Ter Mar 26, 2013 11:52
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





