por MARCIOESTUDIOSO » Seg Fev 14, 2011 10:33
por MARCIOESTUDIOSO » Seg Fev 14, 2011 10:33
Olá Amigos!
Tudo bem?
Estou entrando em contato porque eu fiz essa derivada, e não está batendo com gabarito de resposta, gostaria que em ajudasse a resolver e me mostrasse aonde estou errando por favor.
mais antes veja o que fiz
u=tg(x)
du=sec²(x)dx
?tg³(x)sec²(x)dx=
?u³du=
(u^3)/3+c=
tg^3(x)/3
3x2.34
?
não consigo entender aonde to errando?
se pode me ajudar por favor.
Não posso criar novos tópicos, não entendi motivo mesmo
gostaria de resposta sobre isso..
e para evitar problemas, tirei questão em anexo.
vou escrever.
? (3 sec x tgx - 5 cos sec^2 x) dx
Bom tah ai!
se pode me ajudar me orientando, não fazendo para "mim" eu agradeço!
Editado pela última vez por
MARCIOESTUDIOSO em Seg Fev 14, 2011 20:08, em um total de 2 vezes.
-
MARCIOESTUDIOSO
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Fev 14, 2011 10:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: cursando
 por MARCIOESTUDIOSO » Seg Fev 14, 2011 19:52
por MARCIOESTUDIOSO » Seg Fev 14, 2011 19:52
Não entendi!!
eu tentei fazer?
porque excluir?
eu só coloquei anunciado em anexo?
gostaria saber porque motivo disso?
-
MARCIOESTUDIOSO
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Fev 14, 2011 10:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: cursando
 por LuizAquino » Ter Fev 15, 2011 01:08
por LuizAquino » Ter Fev 15, 2011 01:08
Exercício 1:
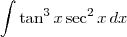
Seja
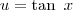
. Desse modo,
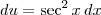
. Portanto, temos que
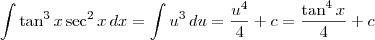 Exercício 2
Exercício 2:
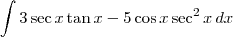
Como
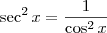
, então essa integral é o mesmo que:
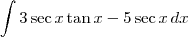
Separando em duas:
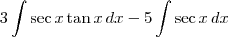
Para resolver a primeira, basta lembrar que
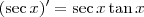
.
Para resolver a segunda, há um truque algébrico. Devemos multiplicar e dividir o integrando por

. Ou seja, teremos:
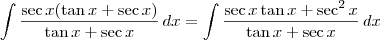
Agora, fazendo a substituição
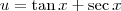
, temos que
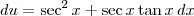
. Portanto, ficamos:
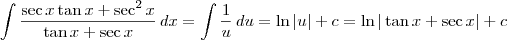
.
Logo, teremos que:
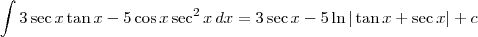
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por MarceloFantini » Ter Fev 15, 2011 12:21
por MarceloFantini » Ter Fev 15, 2011 12:21
Luiz: interessante esse truque. É algo famoso? Eu não tive isso no meu curso de cálculo 1.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por LuizAquino » Ter Fev 15, 2011 14:37
por LuizAquino » Ter Fev 15, 2011 14:37
Olá Fantini,
Não sei a origem desse truque. Foi algo que aprendi quando fiz o curso de Cálculo I. Inclusive, se você procurar pelo google por "integral da secante" irá encontrar muitas páginas ensinando o truque.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Derivada/Integral resolução lista exercícios
 por dimas_ant » Dom Dez 22, 2013 13:33
por dimas_ant » Dom Dez 22, 2013 13:33
- 0 Respostas
- 1515 Exibições
- Última mensagem por dimas_ant

Dom Dez 22, 2013 13:33
Cálculo: Limites, Derivadas e Integrais
-
- Integral - Resolução de integral indefinida.
por brunoisoppo » Qui Mar 03, 2016 15:26
- 0 Respostas
- 3452 Exibições
- Última mensagem por brunoisoppo

Qui Mar 03, 2016 15:26
Cálculo: Limites, Derivadas e Integrais
-
- Problema com resolução da derivada de uma função
por DavidUserCalc » Qua Mar 31, 2010 19:50
- 2 Respostas
- 3198 Exibições
- Última mensagem por DavidUserCalc

Qui Abr 01, 2010 01:19
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada Parcial de 2ª Ordem] - Resolução de Questão
por Vitor2+ » Sáb Jun 30, 2012 23:04
- 3 Respostas
- 3680 Exibições
- Última mensagem por Vitor2+

Dom Jul 01, 2012 11:47
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada-Regra da Cadeia]- Duvidas na resolução
por fabriel » Qui Jun 20, 2013 01:28
- 0 Respostas
- 1204 Exibições
- Última mensagem por fabriel

Qui Jun 20, 2013 01:28
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


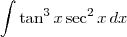
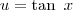 . Desse modo,
. Desse modo, 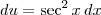 . Portanto, temos que
. Portanto, temos que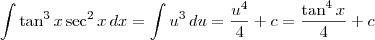
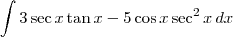
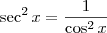 , então essa integral é o mesmo que:
, então essa integral é o mesmo que: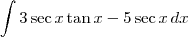
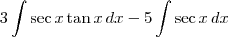
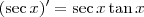 .
. . Ou seja, teremos:
. Ou seja, teremos: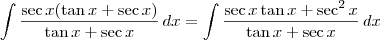
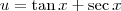 , temos que
, temos que 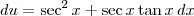 . Portanto, ficamos:
. Portanto, ficamos: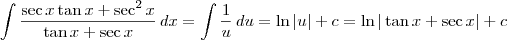 .
.