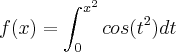
Eu joguei ela no wolfram e me saiu o resultado ,mas nao tinha nenhum step disponível ,pelo que me lembro deu
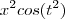 , alguem sabe como chegou nesse resultado ? E se possível explicar o conceito ou a tecnica empregada ?
, alguem sabe como chegou nesse resultado ? E se possível explicar o conceito ou a tecnica empregada ?Agora tem um de limite que também deve ser problema conceitual , o limite é esse :
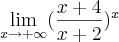
Eu apliquei Logaritmo e tals , depois apliquei l' hopital porque havia uma indeterminação ,mas rodei rodei rodei e nao sai do lugar ,é esse o caminho certo mesmo ?



 logo t = raiz quadrada de u , então fica :
logo t = raiz quadrada de u , então fica :![\frac{1}{2}\int_{0}^{x^2}\frac{cosu}{\sqrt[2]{u}} du \frac{1}{2}\int_{0}^{x^2}\frac{cosu}{\sqrt[2]{u}} du](/latexrender/pictures/455a29e996e067d391efc5581ed98b6c.png)


 multiplicando o
multiplicando o 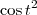 , não tem relação com os limites da integral. Quando usamos substituição, não podemos deixar nada da outra variável sobrando, tudo tem que já estar na integral (salvo números). E outra coisa: quando usamos substituição devemos mudar os limites de integração na integral definida.
, não tem relação com os limites da integral. Quando usamos substituição, não podemos deixar nada da outra variável sobrando, tudo tem que já estar na integral (salvo números). E outra coisa: quando usamos substituição devemos mudar os limites de integração na integral definida.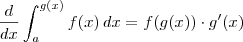
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)