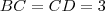 cm,
cm, 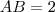 cm, ângulo
cm, ângulo 
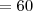 graus e ângulo
graus e ângulo 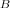
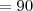 graus. A medida, em cm, do perímetro do quadrilátero é:
graus. A medida, em cm, do perímetro do quadrilátero é:A-( )11
B-( )12
C-( )13
D-( )14
Como fiz:
Tracei as diagonais e depois apliquei o teorema de pitágoras, encontrando o lado x
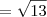 que é aproximadamente
que é aproximadamente 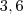 . Somando os lados encontrei o perímetro igual a
. Somando os lados encontrei o perímetro igual a 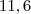 que eu aproximei para resposta 12. Está certo meu raciocínio?Existe outra forma de fazer que não seja aproximado?
que eu aproximei para resposta 12. Está certo meu raciocínio?Existe outra forma de fazer que não seja aproximado?

 está correto...
está correto...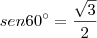 e
e 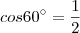 ...
...
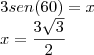
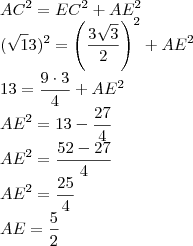



 , avisa que eu resolvo.
, avisa que eu resolvo.

