 por raimundoocjr » Qua Jan 26, 2011 21:21
por raimundoocjr » Qua Jan 26, 2011 21:21
 A priori
A priori não tenho uma base para início. Por favor ajudem-me, desde já obrigado.
-
raimundoocjr
-
 por LuizAquino » Qua Jan 26, 2011 21:59
por LuizAquino » Qua Jan 26, 2011 21:59
Olá raimundoocjr,
Podemos resumir essa situação na figura abaixo. Note que os segmentos pretos seguem o contorno das folhas, já os vermelhos foram traçados para auxilar na resolução do problema.
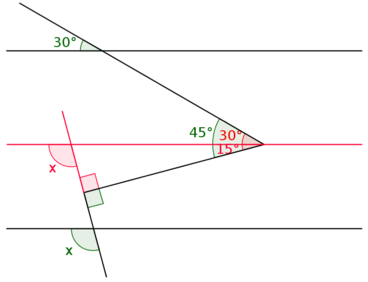
- Construção auxiliar.
- folhas.png (20.87 KiB) Exibido 2050 vezes
É importante você perceber que da figura da questão temos que
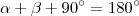
. Como

, então esses ângulos devem ser de 45°.
Em seguida, basta lembrar que x=15°+90°=105°, pois x é ângulo externo no triângulo criado.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por raimundoocjr » Qui Jan 27, 2011 15:40
por raimundoocjr » Qui Jan 27, 2011 15:40
Muitíssimo obrigado.
-
raimundoocjr
-
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Geometria Plana] Qual é o comprimento "D" desse hexágono
 por Marcosd » Qui Jan 28, 2016 15:24
por Marcosd » Qui Jan 28, 2016 15:24
- 4 Respostas
- 5892 Exibições
- Última mensagem por adauto martins

Dom Jan 31, 2016 20:26
Geometria Plana
-
- Geometria Plana - "150º, 160º, 40º e x"
 por raimundoocjr » Ter Jan 25, 2011 20:36
por raimundoocjr » Ter Jan 25, 2011 20:36
- 4 Respostas
- 2737 Exibições
- Última mensagem por Renato_RJ

Qua Jan 26, 2011 21:54
Geometria Plana
-
- Geometria Plana - "Círculo Inscrito"
por raimundoocjr » Sáb Fev 12, 2011 16:18
- 2 Respostas
- 2077 Exibições
- Última mensagem por raimundoocjr

Dom Fev 13, 2011 09:15
Geometria Plana
-
- Geometria Plana - "Área Máxima"
por raimundoocjr » Sex Out 21, 2011 20:30
- 2 Respostas
- 4960 Exibições
- Última mensagem por saberdigitalnet

Sáb Nov 24, 2012 17:19
Geometria Plana
-
- Geometria Plana - "Valor de RQ"
por raimundoocjr » Ter Fev 15, 2011 21:54
- 2 Respostas
- 1953 Exibições
- Última mensagem por raimundoocjr

Qua Fev 16, 2011 13:49
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



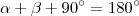 . Como
. Como  , então esses ângulos devem ser de 45°.
, então esses ângulos devem ser de 45°.
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.