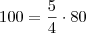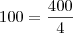por Cleyson007 » Seg Jul 21, 2008 14:05
por Cleyson007 » Seg Jul 21, 2008 14:05
Olá, boa tarde! Fábio, estou com uma dúvida na resolução da questão abaixo apresentada:
O ângulo igual a

do seu suplemento mede quanto?
Eu a resolvi de dois modos, porém as respostas ficaram diferentes. Há alguma correta? qual? e por quê?
O 1º modo que usei foi:
Chamei o ângulo de x

x=
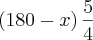

x= 100º
O 2º modo que utilizei foi:
x= (x-180)


x=900º
Por favor ajude-me, pois, não sei qual está certa ou se ambas estão erradas.
Obrigado
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por admin » Seg Jul 21, 2008 14:30
por admin » Seg Jul 21, 2008 14:30
Olá, boa tarde.
O primeiro modo está correto pois a equação representa exatamente a condição do enunciado.
Dois ângulos são suplementares se a soma de suas medidas é 180º.
Você mesmo poderia testar qual valor está correto, por exemplo:
Se 100º é o ângulo, seu suplementar é 80º (pois 100+80 = 180).
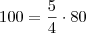
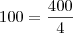

-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- geometria espacial
por Gir » Seg Jul 27, 2009 11:46
- 3 Respostas
- 11735 Exibições
- Última mensagem por Molina

Ter Jul 28, 2009 15:21
Problemas do Cotidiano
-
- Geometria espacial
por nathy vieira » Qua Out 07, 2009 22:37
- 2 Respostas
- 2844 Exibições
- Última mensagem por nathy vieira

Qua Out 07, 2009 23:03
Geometria Espacial
-
- geometria espacial
por nathy vieira » Qua Out 07, 2009 23:18
- 4 Respostas
- 6143 Exibições
- Última mensagem por nathy vieira

Qui Out 08, 2009 18:37
Geometria Espacial
-
- Geometria espacial
por crixprof » Qui Out 15, 2009 10:40
- 2 Respostas
- 3157 Exibições
- Última mensagem por crixprof

Sex Out 16, 2009 18:27
Geometria Espacial
-
- Geometria Espacial
por geriane » Sáb Abr 03, 2010 10:39
- 4 Respostas
- 4201 Exibições
- Última mensagem por geriane

Dom Abr 04, 2010 10:29
Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 do seu suplemento mede quanto?
do seu suplemento mede quanto? x=
x= 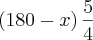
 x= 100º
x= 100º
 x=900º
x=900º