[Medida de ângulo]

AjudaMatematica.com! Aqui você compartilha sua dúvida ou solução!

  • Anúncio Global
    Respostas
    Exibições
    Última mensagem

[Medida de ângulo]

Regras do fórum
Responder

[Medida de ângulo]

Mensagempor Gustavo Gomes » Sex Jan 31, 2014 21:50

Olá, Pessoal!

Na figura a seguir, o triângulo equilátero ABC e o pentágono regular ADEFG possuem lados de mesmo comprimento e estão em posição tal que as retas BC e GF são paralelas.
Quanto mede o ângulo ACD?

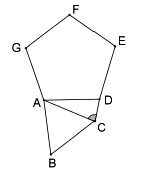
imagem.PNG
imagem.PNG (4.4 KiB) Exibido 2777 vezes


A resposta é 78º.

Considerei a medida dos ângulos internos do pentágono regular e do Triângulo equilátero; tentei prolongar os segmentos AC e GF e trabalhar com ângulos complementares e opostos pelo vértice, mas não consegui chegar no resultado.

Aguardo, grato.
Gustavo Gomes
Usuário Parceiro
Usuário Parceiro
 
Mensagens: 50
Registrado em: Sex Out 05, 2012 22:05
Formação Escolar: PÓS-GRADUAÇÃO
Área/Curso: Matemática-Licenciatura
Andamento: formado
Voltar ao topo

Re: [Medida de ângulo]

Mensagempor young_jedi » Ter Fev 18, 2014 12:24

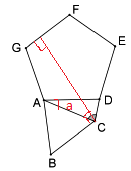
equilateros.png
equilateros.png (5.38 KiB) Exibido 2733 vezes

como as retas são paralelas então podemos traçar uma reta perpendicular com angulo de 90º com ambas
como o angulo do triangulo é 60º então ao angulo entre as retas GC e CA é 30º
então pela soma dos angulos internos do quadrilatero temos

90+30+108+108+a=360

a=24

como o trianulo ACD é isoceles pois possui dois lados inguais então

A\hat{C}D=\frac{180-24}{2}

A\hat{C}D=78^o
young_jedi
Colaborador Voluntário
Colaborador Voluntário
 
Mensagens: 1239
Registrado em: Dom Set 09, 2012 10:48
Formação Escolar: GRADUAÇÃO
Área/Curso: Engenharia Elétrica - UEL
Andamento: formado
Voltar ao topo
Responder

Voltar para Geometria Plana

 


Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!

  • Tópicos relacionados
    Respostas
    Exibições
    Última mensagem

Quem está online

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 


Tópico Popular

Assunto: [Função] do primeiro grau e quadratica
Autor: Thassya - Sáb Out 01, 2011 16:20

1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?

2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?

3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?

Assunto: [Função] do primeiro grau e quadratica
Autor: Neperiano - Sáb Out 01, 2011 19:46

Ola

Qual as suas dúvidas?

O que você não está conseguindo fazer?

Nos mostre para podermos ajudar

Atenciosamente

Assunto: [Função] do primeiro grau e quadratica
Autor: joaofonseca - Sáb Out 01, 2011 20:15

1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.

y_{b}-y_{a}=m(x_{b}-x_{a})

1-3=m(-3-1) \Leftrightarrow -2=-4m \Leftrightarrow m=\frac{2}{4} \Leftrightarrow m=\frac{1}{2}

Em y=mx+b substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.

3=\frac{1}{2} \cdot 1+b\Leftrightarrow 3-\frac{1}{2}=b \Leftrightarrow b=\frac{5}{2}



2)Na equação y=x^2-5x+9 não existem zeros.Senão vejamos

Completando o quadrado,

(x^2-5x+\frac{25}{4})+9-\frac{25}{4} =0\Leftrightarrow (x-\frac{5}{2})^2+\frac{11}{4}=0

As coordenadas do vertice da parabola são (\frac{5}{2},\frac{11}{4})

O eixo de simetria é a reta x=\frac{5}{2}.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.

f(-7)=93
f(10)=59

Powered by phpBB © phpBB Group.

phpBB Mobile / SEO by Artodia.

Índice do fórum