 por Balanar » Sex Out 15, 2010 21:15
por Balanar » Sex Out 15, 2010 21:15
Na figura, temos:
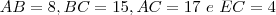
Determine:
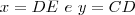

Resposta:
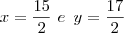 Resolução:
Resolução: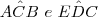
possuem lados respectivamente perpendiculares.
Daí:

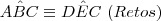
Logo:

Então:
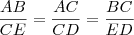
Logo:
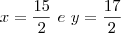
Minha dúvida é a seguinte :
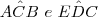
possuem lados respectivamente perpendiculares.
Daí:

Não to prosseguindo ver essa parte.
-
Balanar
- Usuário Parceiro

-
- Mensagens: 72
- Registrado em: Qua Dez 03, 2008 07:18
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Perimetro de 2 triangulos semelhantes
 por aldss » Seg Out 26, 2015 23:34
por aldss » Seg Out 26, 2015 23:34
- 0 Respostas
- 905 Exibições
- Última mensagem por aldss

Seg Out 26, 2015 23:34
Trigonometria
-
- [Geometria Plana - Triângulo] Triângulo Isós. e Bissetriz
por raimundoocjr » Qua Fev 22, 2012 09:41
- 3 Respostas
- 6601 Exibições
- Última mensagem por DanielFerreira

Sáb Fev 25, 2012 01:37
Geometria Plana
-
- Triangulo
por ginrj » Ter Abr 28, 2009 20:58
- 3 Respostas
- 3790 Exibições
- Última mensagem por ginrj

Sáb Mai 02, 2009 12:30
Geometria Plana
-
- Triângulo.
por Molina » Qua Mai 13, 2009 23:20
- 2 Respostas
- 2151 Exibições
- Última mensagem por Molina

Qui Mai 14, 2009 19:04
Geometria Plana
-
- Triângulo
por cristina » Seg Set 14, 2009 18:49
- 5 Respostas
- 3033 Exibições
- Última mensagem por Marcampucio

Ter Set 15, 2009 16:44
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
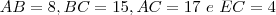
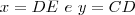

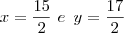
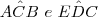 possuem lados respectivamente perpendiculares.
possuem lados respectivamente perpendiculares.
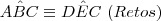

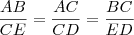
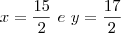
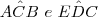 possuem lados respectivamente perpendiculares.
possuem lados respectivamente perpendiculares.

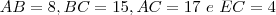
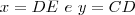

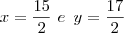
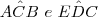 possuem lados respectivamente perpendiculares.
possuem lados respectivamente perpendiculares.
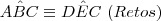

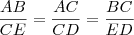
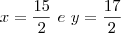
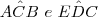 possuem lados respectivamente perpendiculares.
possuem lados respectivamente perpendiculares.



 , avisa que eu resolvo.
, avisa que eu resolvo.

