 por nayane » Sex Set 10, 2010 11:01
por nayane » Sex Set 10, 2010 11:01
A razão entre a área do quadrado circunscrito e a área do quadrado inscrito no mesmo círculo?
Nayane
-

nayane
- Usuário Dedicado

-
- Mensagens: 31
- Registrado em: Sex Set 10, 2010 10:42
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em ciências biológicas
- Andamento: cursando
 por nayane » Sáb Set 11, 2010 20:12
por nayane » Sáb Set 11, 2010 20:12
Muito obrigada, sua ajuda foi muito importante.

Nayane
-

nayane
- Usuário Dedicado

-
- Mensagens: 31
- Registrado em: Sex Set 10, 2010 10:42
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em ciências biológicas
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- como se faz isso
por Amandatkm » Dom Abr 28, 2013 17:50
- 1 Respostas
- 2790 Exibições
- Última mensagem por young_jedi

Seg Abr 29, 2013 12:42
Aritmética
-
- como resolvo isso
por weverton » Dom Jul 18, 2010 23:56
- 1 Respostas
- 1595 Exibições
- Última mensagem por MarceloFantini

Seg Jul 19, 2010 03:18
Estatística
-
- Como provo isso?
por MariaPaulaGC » Qui Mar 22, 2012 16:50
- 2 Respostas
- 1502 Exibições
- Última mensagem por MariaPaulaGC

Qui Mar 22, 2012 20:22
Trigonometria
-
- Como posso resolver isso????
por Mimizinha » Qui Mar 20, 2008 10:15
- 6 Respostas
- 6591 Exibições
- Última mensagem por Mimizinha

Qui Mar 20, 2008 13:15
Geometria Analítica
-
- tem como resolver isso sem usar calculadora?
por weverton » Sáb Jul 24, 2010 06:07
- 3 Respostas
- 2334 Exibições
- Última mensagem por Neperiano

Seg Jul 26, 2010 00:36
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



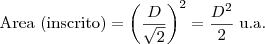
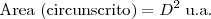
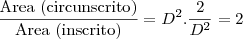



 .
.
 :
: