Calculo da trajetoriade uma imagem no espelho

[robertomarinho]

Este problema estava em uma prova do IFRJ cujo conteudo era do ensino fundamental:

"Fernanda se encontrava distante meio metro do espelho, antes de ele ter girado, com sua imagem centralizada. O espelho girou 15°, afastando-se dela. Sua imagem se deslocou, descrevendo um caminho. Sabendo-se que o meu espelho é retangular, de dimensões 1 m xl, 7m e que ocupa toda a porta do armário, determine a natureza do caminho descrito pela imagem e o seu comprimento em metros."

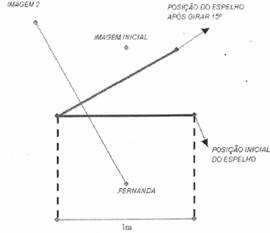
Imagem do problema

image002.jpg (4.51 KiB) Exibido 1320 vezes

Soluções

image004.jpg (14.28 KiB) Exibido 1319 vezes

Gente eu confesso que postaria minhas tentativas, mas eu não faço a mais pálida idéia de como resolver este problema.
Meu prof de matemática tambem não soube.
Agradeço muuuuiiito desde já e um abraço para todos que tentarem.

Atenciosamente,
Roberto Marinho

[Elcioschin]

Na verdade é bem simples, desde que bem analisado.

Faça um bom desenho em escala:

Seja VE o espelho (V é o vértice esquerdo fixo) ----> VE = 1m
Seja M o ponto médio do espelho.
Seja F a Fernanda ----> FM = 0,5m
Seja G a imagem de Fernanda ---> GM = 1 m
Desenhe agora o espelho VE' na nova posição ----> ^EVE' = 15º
Por F trace uma perpendicular ao espelho na nova posição. Seja N o pé da perpendicular sobre o espelho
Meça a distância FN. Prolongue FN até um ponto H tal que HN = FN. H é a nova imagem de Fernanda.

Se você esolher mais alguns ângulos verá que a imagem de Fernanda descreve um arco de circunferência. Comece com o espelho encostado em Fernanda (neste caso a imagem coincide com ela)

Triângulo retângulo FMV ----> VF² = VM² + FM² -----> VF² = (1/2)² + (1/2)² ----> VF² = 1/2 ----> VF = V2/2

VF é o raio r da circunferência que a imagem descreve.

Ângulo GFH = Ângulo EVE' (lados respectimente perpendiculares) -----> ^GFH = 15º

O ângulo GFH é um ângulo inscrito na circunferência citada. Logo, o arco GH vale ----> Arco GH = 2*15º = 30º

Agora é uma simples regra de três:

180º ----- pi*r
30º ------- x

x = (30º/180º)*pi*r ----> x = pi*r/6 ----> x = pi(V2/2) ----> x = pi*V2/12 ----> Alternativa D

[robertomarinho]

Dúvida respondida. Muito Obrigado.