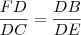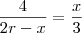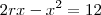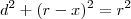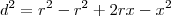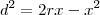por heldersmd » Sáb Set 15, 2012 17:06
por heldersmd » Sáb Set 15, 2012 17:06
Muito obrigado pela resposta anterior!!!!
Na questão:
Seja um triângulo BAC inscrito em uma semicircunferência de diâmetro BC. Uma reta perpendicular a BC, em um ponto D, corta a reta suporte do lado AB no ponto E, a reta suporte do lado AC no ponto F e a semicircunferência no ponto H. Calcule DH sabendo que DE = 3 cm e que DF = 4 cm.
Cheguei a tres triangulos semelhantes, utilizei o ponto FA vezes FC igual a FH vezes o prolongamento de D; tentei pela trigonometria, mas não consegui chegar a lugar algum...
Mais uma vez muito obrigado!!!!!!
-
heldersmd
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sex Set 14, 2012 16:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: vestibulando
- Andamento: cursando
 por young_jedi » Sáb Set 15, 2012 21:07
por young_jedi » Sáb Set 15, 2012 21:07
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Triângulo e Círculo]
 por Mayra Luna » Qua Out 17, 2012 19:46
por Mayra Luna » Qua Out 17, 2012 19:46
- 2 Respostas
- 1553 Exibições
- Última mensagem por Mayra Luna

Qua Out 17, 2012 20:09
Trigonometria
-
- Triangulo circunscrito no circulo
por leandrynhucarioca » Seg Ago 15, 2011 23:55
- 0 Respostas
- 1103 Exibições
- Última mensagem por leandrynhucarioca

Seg Ago 15, 2011 23:55
Geometria Plana
-
- Círculo trigonométrico
 por Ananda » Sex Fev 29, 2008 10:56
por Ananda » Sex Fev 29, 2008 10:56
- 8 Respostas
- 7545 Exibições
- Última mensagem por Ananda

Seg Mar 03, 2008 17:51
Trigonometria
-
- Círculo trigonométrico
 por Ananda » Qui Mar 06, 2008 23:00
por Ananda » Qui Mar 06, 2008 23:00
- 1 Respostas
- 3708 Exibições
- Última mensagem por Neperiano

Dom Set 04, 2011 22:07
Geometria
-
- Círculo Trigonométrico
por caiolasagno » Seg Abr 13, 2009 21:18
- 1 Respostas
- 2318 Exibições
- Última mensagem por Marcampucio

Seg Abr 13, 2009 21:29
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.