por maria cleide » Qui Out 13, 2011 11:33
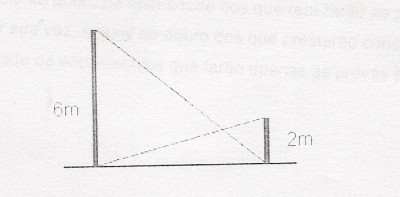
Em uma exposição artística um escultor apresentou sua obra prima, intitulanda "as torres vizinhas". Repare que a mesma consta de duas hastes paralelas de ferro fundidas perpendicularmente em uma mesma base e escoradas por dois cabos de aço retilíneos, como mostra a figura abaixo. As alturas das hastes medem, respectivamente, 6 metros e 2 metros. Desprezando-se a espesura dos cabos, determine a distância do ponto de interseção dos cabos à base da escultura.
Eu consegui encontra dois triângulos cujas bases são 6 e 2, mas não consegui desenvolver isto.
- Anexos
-
-
maria cleide
- Usuário Parceiro
-
- Mensagens: 54
- Registrado em: Dom Mai 08, 2011 12:57
- Formação Escolar: ENSINO FUNDAMENTAL I
- Andamento: cursando
por maria cleide » Sex Out 14, 2011 22:43
Por favor, me ajudem.
Obrigada M.C.
-
maria cleide
- Usuário Parceiro
-
- Mensagens: 54
- Registrado em: Dom Mai 08, 2011 12:57
- Formação Escolar: ENSINO FUNDAMENTAL I
- Andamento: cursando
Voltar para Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30
Então, o exercicio pede para encontrar
.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:
Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):
Somando a primeira e a segunda equação:
Finalmente:
Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
