por angsrom » Dom Mai 15, 2011 12:45
Olá, minha primeira postagem no fórum!
Bom..estou tentando fazer esta questão a um tempo, mas ainda não consegui solucioná-la:
Qual é o resultado de k, sabendo que k=sen1234pi/cos3457pi/2?
Tipo eu tente fazer suposições usando o primeiro e o último número para reduzir o valo.
Como por exemplo:
sen1234pi = sen1pi (por causa do 1)
e
sen1234pi = sen4pi (por causa do 4)
Mas... não coincidiu, os valores são completamente diferentes para fazer este tipo de semelhança.
Editado pela última vez por
angsrom em Dom Mai 15, 2011 14:49, em um total de 2 vezes.
-
angsrom
- Novo Usuário
-
- Mensagens: 4
- Registrado em: Dom Mai 15, 2011 12:29
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
por FilipeCaceres » Dom Mai 15, 2011 13:36
Se você encontrou
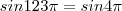
Basta saber que
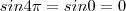
Comos
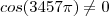
Portanto,
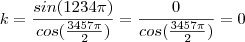
Abraço.
-
FilipeCaceres
- Colaborador Voluntário
-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
por angsrom » Dom Mai 15, 2011 14:53
Entendi. Talvez o único problema seje a percepção na hora de comparar entre os valores na função anti-horária de pi.
Detalhe para complementar, sim tem uma opção na questão com o valor 0.
Agora vou testar com outros valores, Obrigado!
-
angsrom
- Novo Usuário
-
- Mensagens: 4
- Registrado em: Dom Mai 15, 2011 12:29
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Quais os possíveis valores que satisfazem os valores reais
por andersontricordiano » Seg Fev 24, 2014 22:53
- 1 Respostas
- 5041 Exibições
- Última mensagem por Russman
Ter Fev 25, 2014 02:17
Números Complexos
-
- Os valores de x são?
por Killder » Ter Nov 27, 2012 08:11
- 1 Respostas
- 2702 Exibições
- Última mensagem por Neperiano
Ter Nov 27, 2012 15:09
Álgebra Elementar
-
- valores: x e de y
por Victor Gabriel » Dom Abr 21, 2013 16:02
- 1 Respostas
- 2464 Exibições
- Última mensagem por Luis Gustavo
Seg Mai 06, 2013 16:48
Aritmética
-
- valores de a e b
por brunoguim05 » Qua Mai 28, 2014 15:34
- 0 Respostas
- 1172 Exibições
- Última mensagem por brunoguim05
Qua Mai 28, 2014 15:34
Geometria Analítica
-
- Soma dos valores de x
por thadeu » Qui Nov 19, 2009 11:49
- 0 Respostas
- 1045 Exibições
- Última mensagem por thadeu
Qui Nov 19, 2009 11:49
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 09:10
Veja este exercício:
Se A = {
} e B = {
}, então o número de elementos A
B é:
Eu tentei resolver este exercício e achei a resposta "três", mas surgiram muitas dúvidas aqui durante a resolução.
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero?
existe inverso de zero?
zero é par, certo?
sendo x um número natural, -x é múltiplo de x?
sendo z um número inteiro negativo, z é múltiplo de z?
sendo z um número inteiro negativo, -z é múltiplo de z?
A resposta é 3?
Obrigado.
Assunto:
método de contagem
Autor:
Molina - Seg Mai 25, 2009 20:42
Boa noite, sinuca.
Se A = {
} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
Ou seja, quais são os divisores de 20? Eles são seis: 1, 2, 4, 5, 10 e 20.
Logo, o conjunto A é
A = {1, 2, 4, 5, 10, 20}
Se B = {
} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
Logo, o conjunto B é
B = {... , -25, -20, -15, -10, -5, 0, 5, 10, 15, 20, 25, ...
Feito isso precisamos ver os números que está em ambos os conjuntos, que são:
5, 10 e 20 (3 valores, como você achou).
Vou responder rapidamente suas dúvidas porque meu tempo está estourando. Qualquer dúvida, coloque aqui, ok?
sinuca147 escreveu:No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero? sim, é o próprio zero
existe inverso de zero? não, pois não há nenhum número que multiplicado por zero resulte em 1
zero é par, certo? sim, pois pode ser escrito da forma de 2n, onde n pertence aos inteiros
sendo x um número natural, -x é múltiplo de x? Sim, pois basta pegar x e multiplicar por -1 que encontramos -x
sendo z um número inteiro negativo, z é múltiplo de z? Sim, tais perguntando se todo número é multiplo de si mesmo
sendo z um número inteiro negativo, -z é múltiplo de z? Sim, pois basta pegar -z e multiplicar por -1 que encontramos x
A resposta é 3? Sim, pelo menos foi o que vimos a cima
Bom estudo,
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 23:35
Obrigado, mas olha só este link
http://www.colegioweb.com.br/matematica ... ro-natural
neste link encontra-se a a frase:
Múltiplo de um número natural é qualquer número que possa ser obtido multiplicando o número natural por 0, 1, 2, 3, 4, 5, etc.
Para determinarmos os múltiplos de 15, por exemplo, devemos multiplicá-lo pela sucessão dos números naturais:
Ou seja, de acordo com este link -5 não poderia ser múltiplo de 5, assim como 5 não poderia ser múltiplo de -5, eu sempre achei que não interessava o sinal na questão dos múltiplos, assim como você me confirmou, mas e essa informação contrária deste site, tem alguma credibilidade?
Há e claro, a coisa mais bacana você esqueceu, quero saber se existe algum método de contagem diferente do manual neste caso:
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
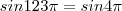
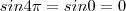
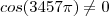
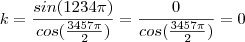
