 por c_zaidan » Qui Dez 09, 2010 11:33
por c_zaidan » Qui Dez 09, 2010 11:33
Um curral retangular será construído aproveitando-se um muro pré-existente no terreno, por medida de economia. Para cercar os outros lados, serão utilizados 600m de tela de arame. Para que a área do curral seja a maior possível, a razão entre as suas menor e maior dimensões será:
Chamei a medida do muro de x e do outro lado de 600-x, mas travou e nn consegui desenvolver mais. Será q dá pra me dar uma dica, ou ver o q eu to errando?
Valeu
-
c_zaidan
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sex Out 22, 2010 15:40
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por alexandre32100 » Qui Dez 09, 2010 16:20
por alexandre32100 » Qui Dez 09, 2010 16:20
Temos o seguinte esquema
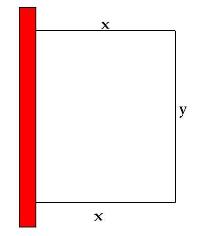
- a parte em vermelho representa o muro
- cerca.JPG (4.02 KiB) Exibido 3455 vezes
Onde
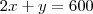
ou
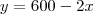
Como a área do retângulo é dada por
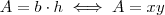
Podemos fazer a substituição e obter
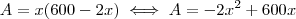
É necessário agora apenas encontrar o valor de
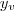
(

do vértice).
-
alexandre32100
-
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Razão da área do triângulo para a área do quadrilátero]
 por Mayra Luna » Sex Nov 23, 2012 20:17
por Mayra Luna » Sex Nov 23, 2012 20:17
- 2 Respostas
- 4422 Exibições
- Última mensagem por Mayra Luna

Ter Nov 27, 2012 14:53
Geometria Plana
-
- Área - Na próxima figura ABCD é um quadrilátero de área 200
 por marguiene » Sex Out 10, 2014 10:22
por marguiene » Sex Out 10, 2014 10:22
- 0 Respostas
- 2133 Exibições
- Última mensagem por marguiene

Sex Out 10, 2014 10:22
Geometria Plana
-
- Área - Na figura abaixo ABCD é um retângulo de área 11 cm².
 por marguiene » Sex Out 10, 2014 10:35
por marguiene » Sex Out 10, 2014 10:35
- 0 Respostas
- 2904 Exibições
- Última mensagem por marguiene

Sex Out 10, 2014 10:35
Geometria Plana
-
- [Área] Área de triangulo e trapézio
 por smlspirit » Qui Jul 19, 2012 20:07
por smlspirit » Qui Jul 19, 2012 20:07
- 1 Respostas
- 3001 Exibições
- Última mensagem por e8group

Qui Jul 19, 2012 20:57
Geometria Plana
-
- Area
por karenblond » Qui Mar 25, 2010 17:19
- 6 Respostas
- 4176 Exibições
- Última mensagem por Molina

Ter Mar 30, 2010 00:35
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


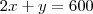 ou
ou 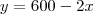
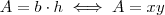
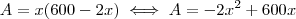
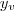 (
( do vértice).
do vértice).
 .
.



