por Gustavo Gomes » Sáb Fev 15, 2014 22:01
Ola!
Em um cubo de volume V, sejam F1 e F2 duas faces paralelas. Uma pirâmide tem F1 como base e vértice no centro de F2 e outra pirâmide tem F2 como base e vértice no centro de F1.
Qual o volume da parte comum a essas pirâmides?
A resposta é V/12.
Não estou conseguindo definir a área da secção que representa a base dessas partes comuns....
Aguardo. Grato.
-
Gustavo Gomes
- Usuário Parceiro
-
- Mensagens: 50
- Registrado em: Sex Out 05, 2012 22:05
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática-Licenciatura
- Andamento: formado
por young_jedi » Dom Fev 16, 2014 19:41
as piramedes se interceptam no centro do cubo portanto a metade superior de cada piramede esta contida dentro da outra sendo esta a região comum entre elas
temos portanto que calcular o volume da metade superior de cada uma das metades superiores
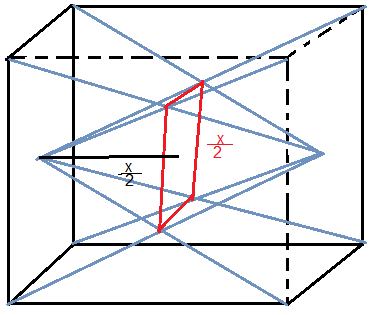
- piram.png (7.06 KiB) Exibido 2762 vezes
sendo o lado do quadrado igual a x então a altura dessas piramdes sera x/2 e o lado da base por semelhança de triangulos tambem sera x/2
portanto o volume de cada uma sera
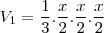
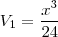
como o volume comum é a soma do volume das duas piramedes então
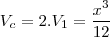
mais como
-
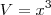
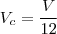
young_jedi
- Colaborador Voluntário
-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Geometria Espacial
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [cubo e pirâmides] Questão difícil
por plugpc » Qua Jul 16, 2008 18:16
- 4 Respostas
- 5363 Exibições
- Última mensagem por admin
Qui Jul 17, 2008 00:45
Geometria Espacial
-
- CUBO E PIRAMIDES....QUESTAO PRA FERA
por carolcmalta » Qui Out 08, 2009 05:04
- 2 Respostas
- 5616 Exibições
- Última mensagem por carolcmalta
Qui Out 08, 2009 14:06
Geometria Espacial
-
- volume do cubo
por irineu junior » Sex Mar 12, 2010 21:32
- 1 Respostas
- 1942 Exibições
- Última mensagem por Elcioschin
Sáb Mar 13, 2010 15:06
Geometria Espacial
-
- [volume do cubo] Soma dos volumes das infinitas caixas
por Priscilamoraes307 » Sex Ago 10, 2012 23:14
- 2 Respostas
- 2197 Exibições
- Última mensagem por Russman
Sáb Ago 11, 2012 16:08
Geometria Espacial
-
- PIRAMIDES
por guhh » Qui Ago 13, 2009 23:19
- 1 Respostas
- 2336 Exibições
- Última mensagem por Molina
Sex Ago 14, 2009 14:37
Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 09:10
Veja este exercício:
Se A = {
} e B = {
}, então o número de elementos A
B é:
Eu tentei resolver este exercício e achei a resposta "três", mas surgiram muitas dúvidas aqui durante a resolução.
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero?
existe inverso de zero?
zero é par, certo?
sendo x um número natural, -x é múltiplo de x?
sendo z um número inteiro negativo, z é múltiplo de z?
sendo z um número inteiro negativo, -z é múltiplo de z?
A resposta é 3?
Obrigado.
Assunto:
método de contagem
Autor:
Molina - Seg Mai 25, 2009 20:42
Boa noite, sinuca.
Se A = {
} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
Ou seja, quais são os divisores de 20? Eles são seis: 1, 2, 4, 5, 10 e 20.
Logo, o conjunto A é
A = {1, 2, 4, 5, 10, 20}
Se B = {
} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
Logo, o conjunto B é
B = {... , -25, -20, -15, -10, -5, 0, 5, 10, 15, 20, 25, ...
Feito isso precisamos ver os números que está em ambos os conjuntos, que são:
5, 10 e 20 (3 valores, como você achou).
Vou responder rapidamente suas dúvidas porque meu tempo está estourando. Qualquer dúvida, coloque aqui, ok?
sinuca147 escreveu:No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero? sim, é o próprio zero
existe inverso de zero? não, pois não há nenhum número que multiplicado por zero resulte em 1
zero é par, certo? sim, pois pode ser escrito da forma de 2n, onde n pertence aos inteiros
sendo x um número natural, -x é múltiplo de x? Sim, pois basta pegar x e multiplicar por -1 que encontramos -x
sendo z um número inteiro negativo, z é múltiplo de z? Sim, tais perguntando se todo número é multiplo de si mesmo
sendo z um número inteiro negativo, -z é múltiplo de z? Sim, pois basta pegar -z e multiplicar por -1 que encontramos x
A resposta é 3? Sim, pelo menos foi o que vimos a cima
Bom estudo,
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 23:35
Obrigado, mas olha só este link
http://www.colegioweb.com.br/matematica ... ro-natural
neste link encontra-se a a frase:
Múltiplo de um número natural é qualquer número que possa ser obtido multiplicando o número natural por 0, 1, 2, 3, 4, 5, etc.
Para determinarmos os múltiplos de 15, por exemplo, devemos multiplicá-lo pela sucessão dos números naturais:
Ou seja, de acordo com este link -5 não poderia ser múltiplo de 5, assim como 5 não poderia ser múltiplo de -5, eu sempre achei que não interessava o sinal na questão dos múltiplos, assim como você me confirmou, mas e essa informação contrária deste site, tem alguma credibilidade?
Há e claro, a coisa mais bacana você esqueceu, quero saber se existe algum método de contagem diferente do manual neste caso:
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
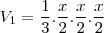
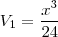
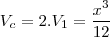
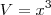
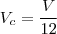
