Escreva uma equação do plano paralelo ao eixo z e que contém os pontos A(2,0,0) e B(0,3,2)
Gabarito:
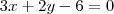
Resolvi da seguinte forma:
Como o plano é paralelo ao eixo z, sabe-se que o vetor
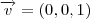 é pertencente ao plano, mas no meu ponto de vista, este (0,0,1) também é um ponto pertencente ao plano, então usei C(0,0,1). Portanto agora tenho 3 pontos pertencentes ao plano.
é pertencente ao plano, mas no meu ponto de vista, este (0,0,1) também é um ponto pertencente ao plano, então usei C(0,0,1). Portanto agora tenho 3 pontos pertencentes ao plano.Fazendo
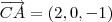 e
e 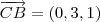 , encontro 2 vetores coplanares e não colineares. Portanto,
, encontro 2 vetores coplanares e não colineares. Portanto,  X
X 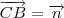
Após fazer o produto escalar dos 2 vetores, obtive que
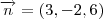
Fazendo
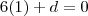 , encontro
, encontro 
Enfim, substituindo, a equação geral do plano que encontrei foi
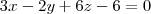 .
.Alguém sabe me explicar o por quê do meu resultado estar diferente do gabarito e se a minha resolução está certa?
Obrigado
Edit:
Aproveitando o tópico, qual a diferença quando um plano é definido pelo eixo z ou o plano é paralelo ao eixo z?


 e
e 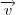
 significa que o vetor normal ao plano é ortogonal ao vetor diretor do eixo. Logo o vetor normal do plano será da forma
significa que o vetor normal ao plano é ortogonal ao vetor diretor do eixo. Logo o vetor normal do plano será da forma 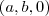 e a equação geral do plano
e a equação geral do plano 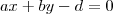 .
.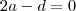 e
e 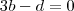 . O que o gabarito fez foi simplesmente facilitar a vida e tomar
. O que o gabarito fez foi simplesmente facilitar a vida e tomar  , de onde segue que
, de onde segue que  e
e  , tornando a equação do plano
, tornando a equação do plano 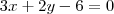 .
.


 .
.
 :
: