Ao resolver um lista de exercicios, durante meus estudos, me deparei com 1 exercicios, que nao consegui resolver, alguem poderia me ajudar neles?
Determinar o valor ? para que o vetor v = (?, -2?, 2?), seja um vetor.
Me ajudem por favor! Obrigado!








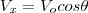

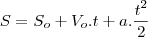
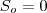 para o eixo y temos que a aceleração é igual a -g, onde g é a gravidade
para o eixo y temos que a aceleração é igual a -g, onde g é a gravidade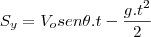
 então
então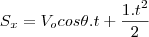

![\sqrt[2]{{a}^{2}+{4a}^{2}+{4a}^{2}}=1
\sqrt[2]{{a}^{2}+{8a}^{2}}=1
\sqrt[2]{{9a}^{2}}=1
{3a}^{2}=1
{a}^{2}=\frac{1}{3}
a=\sqrt[2]{\frac{1}{3}} \sqrt[2]{{a}^{2}+{4a}^{2}+{4a}^{2}}=1
\sqrt[2]{{a}^{2}+{8a}^{2}}=1
\sqrt[2]{{9a}^{2}}=1
{3a}^{2}=1
{a}^{2}=\frac{1}{3}
a=\sqrt[2]{\frac{1}{3}}](/latexrender/pictures/d3c337f72706f2b9bbf95cf1034c0b27.png)



Voltar para Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante