 por Claudin » Qui Jul 05, 2012 19:52
por Claudin » Qui Jul 05, 2012 19:52
Determine e identifique o lugar geométrico dos pontos equidistantes da reta
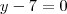
e do ponto
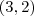
e determine o vértice e a equação do eixo.
Gostaria de saber como iniciar esse exercício, em que tenho uma reta e um ponto.
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Russman » Qui Jul 05, 2012 22:44
por Russman » Qui Jul 05, 2012 22:44
SUponha qe esse ponto é
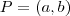
. Calcule a distancia do mesmo até o ponto e do mesmo até a reta. Em seguida, iguale as duas. Veja o que você obtem!
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Claudin » Sex Jul 06, 2012 11:44
por Claudin » Sex Jul 06, 2012 11:44
A distancia do ponto a reta deu
![\frac{5\sqrt[]{13}}{13} \frac{5\sqrt[]{13}}{13}](/latexrender/pictures/6184c6c8b27a625020fa33d81b5bff63.png)
e depois o que fazer
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Russman » Sex Jul 06, 2012 16:48
por Russman » Sex Jul 06, 2012 16:48
Russman escreveu:SUponha qe esse ponto é
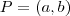
. Calcule a distancia do mesmo até o ponto e do mesmo até a reta. Em seguida, iguale as duas. Veja o que você obtem!
Distancia de
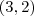
a

:
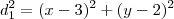
Distância entre a reta
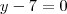
e

:
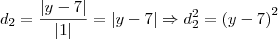
.
Agora, como

, então

e , logo,
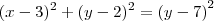
.
Agora desenvolva, estude a função e determine o lugar geométrico, isto é, a superfície plana tal que satisfaz a condição do problema.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Parábola]Determinar vértice de parábola (Urgente!)
por migvas99 » Seg Out 08, 2012 14:37
- 1 Respostas
- 2732 Exibições
- Última mensagem por young_jedi

Seg Out 08, 2012 17:09
Funções
-
- [Parábola] Encontrando o ponto na parábola
por Ana_Rodrigues » Ter Nov 22, 2011 20:44
- 1 Respostas
- 4887 Exibições
- Última mensagem por LuizAquino

Ter Nov 22, 2011 21:38
Geometria Analítica
-
- Parábola
por flavio2010 » Sáb Jul 17, 2010 19:11
- 1 Respostas
- 1933 Exibições
- Última mensagem por Tom

Sáb Jul 17, 2010 22:20
Funções
-
- Parábola
por flavio2010 » Dom Jul 18, 2010 19:42
- 1 Respostas
- 1824 Exibições
- Última mensagem por Tom

Dom Jul 18, 2010 23:31
Funções
-
- Parábola
por flavio2010 » Sex Jul 23, 2010 19:16
- 1 Respostas
- 1930 Exibições
- Última mensagem por MarceloFantini

Sáb Jul 24, 2010 01:40
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
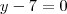 e do ponto
e do ponto 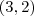 e determine o vértice e a equação do eixo.
e determine o vértice e a equação do eixo.
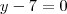 e do ponto
e do ponto 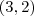 e determine o vértice e a equação do eixo.
e determine o vértice e a equação do eixo.
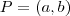 . Calcule a distancia do mesmo até o ponto e do mesmo até a reta. Em seguida, iguale as duas. Veja o que você obtem!
. Calcule a distancia do mesmo até o ponto e do mesmo até a reta. Em seguida, iguale as duas. Veja o que você obtem!
![\frac{5\sqrt[]{13}}{13} \frac{5\sqrt[]{13}}{13}](/latexrender/pictures/6184c6c8b27a625020fa33d81b5bff63.png)

. Calcule a distancia do mesmo até o ponto e do mesmo até a reta. Em seguida, iguale as duas. Veja o que você obtem!
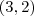 a
a  :
: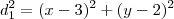
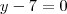 e
e  :
: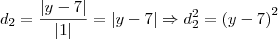 .
. , então
, então  e , logo,
e , logo,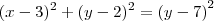 .
.
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.