Bem estou tentando resolver um exercicio sobre subspaço porém não estou conseguindo conclui-lo, bem segue abaixo o exercício e o que consegui resolver até o presente momento. E também gostaria de saber se alguém pode me dizer se estou certa na minha linha de raciocínio...
Considere
S = {( x, y, z ) pertencentes a R³: x = 2y - z }
a) Verifique se S é um subspaço de R3.
b) Exiba uma base de S mostrando que, de fato, tal conjunto é base de S.
c) Ortogonalize a base que você encontrou no itém (b).
Resolução:
a) Seja
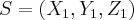 e
e 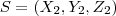
 e
e  , Somando S¹+ S², tem-se
, Somando S¹+ S², tem-se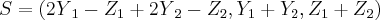 pertencentes a R³
pertencentes a R³*** Condição de existencia x+y pertence a R³ aceita...
Multiplicando por um escalar K...
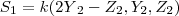
e
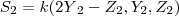 ,
, Logo tem-se:
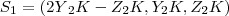
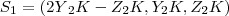
*** Condição de existencia KX pertence a R³ aceita...
*** Condição de existencia
 pertence a R³ aceita, pois o cojunto nulo e solução da equação
pertence a R³ aceita, pois o cojunto nulo e solução da equação 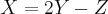 .
.DÚVIDAS!!!!!!!!!!
a) Caso esteje certo, se eu colocar uma resolução assim na prova esta claro ou preciso melhorar algum? O que seria por exemplo???
b) Não sei como vou resolver, queria saber se tem que colocar algum valor intuitivamente ou dá para saber de outra forma?
c) Gostaria de maiores esclarecimentos também da sua fora de resolução...
Agradeço a atenção e se alguem puder me ajudar desde ja agradeço...



 .
.
 :
: