marinalcd escreveu:Seja ABC um triângulo de área 4 tal que AB está contido em r1 e AC está contido em r2, onde r1 = {(t; 3t + 1; 0); com t pertencendo aos reais} e r2 é paralela ao vetor u = (3; 1; 0) e passa pelo ponto M = (3; 2; 0). Determine a equação da reta r3 paralela ao vetor v = (1;-1; 0) que contém o lado BC e determine os vértices A, B e C do triângulo.
marinalcd escreveu:Bom, consegui achar o vértice A , calculando a interseção entre as retas r1 e r2.
Ok. Nesse caso, temos que A = (0, 1, 0).
marinalcd escreveu:tentei usar a fórmula da área do triângulo por determinante, para achar outro vértice, mas não consegui, não deu certo.
Você vai precisar usar o fato de que
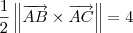
.
marinalcd escreveu:Depois disse que um ponto para montar a equação de r3 seria o mesmo ponto de r2 = (3,2,0). Mas depois parei para pensar e vi que não posso afirmar que o ponto de interseção dentre r2 e r3 é esse.
De fato, você não pode afirmar isso. A final de contas, a interseção entre r2 e r3 deve ser o ponto C. Fazendo a suposição de que r3 passa por (3, 2, 0) (que é um ponto pertencente a r2), você estaria dizendo que C é igual a (3, 2, 0). Mas isso não é verdade.
Vejamos como seguir pelo caminho da área do triângulo.
Pelos dados do exercício, o vetor
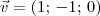
é paralelo a reta r3. Além disso, a reta r3 contém BC. Desse modo, devemos ter
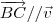
. Isso significa que existe um escalar k tal que
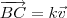
. Portanto, temos que
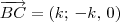
.
Como B pertence a reta r1 e C pertence a reta r2, temos que B = (b; 3b + 1; 0) e C = (3c + 3; c + 2; 0), com b e c sendo algum escalar.
Sendo assim, temos que:
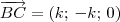
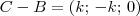


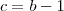
Substituindo c por b - 1 na expressão para o ponto C, temos que C = (3b; b + 1; 0).
Por outro lado, a área de ABC é igual a 4. Isso significa que
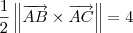
.
Mas sabemos que:
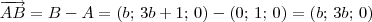
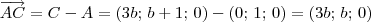
Sendo assim, temos que:
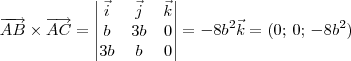
Agora tente continuar o exercício a partir daí.


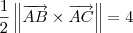 .
.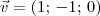 é paralelo a reta r3. Além disso, a reta r3 contém BC. Desse modo, devemos ter
é paralelo a reta r3. Além disso, a reta r3 contém BC. Desse modo, devemos ter 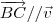 . Isso significa que existe um escalar k tal que
. Isso significa que existe um escalar k tal que 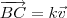 . Portanto, temos que
. Portanto, temos que 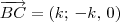 .
.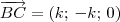
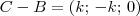


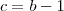
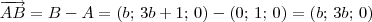
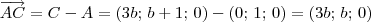
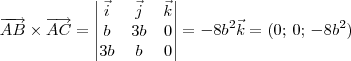

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
