 por leandro_aur » Dom Mar 04, 2012 16:41
por leandro_aur » Dom Mar 04, 2012 16:41
Galera, tenho uma dúvida aqui em um exercício que surgiu. A questão pede o seguinte:
Verifique se em cada um dos itens abaixo o subconjunto W é um subespaço vetorial do espaço vetorial V. Caso não sejam especificadas, as operações são as usuais.
Então galera, o ítem que não consegui provar é o seguinte:
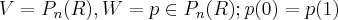
Se fosse p(0)=0 eu poderia usar as demonstrações usuais, só que assim eu já não sei... Alguém pode dar uma ajuda? Valeu
-
leandro_aur
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Dom Out 24, 2010 17:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciencia e Tecnologia
- Andamento: cursando
 por MarceloFantini » Dom Mar 04, 2012 17:04
por MarceloFantini » Dom Mar 04, 2012 17:04
Para provar que isto é subespaço basta mostrar que qualquer combinação linear de polinômios avaliados em zero terão a mesma avaliação quando avaliados em um. Veja:
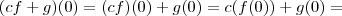
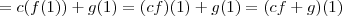
.
Daí é subespaço. Veja que da segunda para a terceira igualdades eu apenas usei que se

e

pertencem ao espaço, sua avalição em zero é igual sua avalição em um.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por leandro_aur » Dom Mar 04, 2012 17:09
por leandro_aur » Dom Mar 04, 2012 17:09
Entendi, então só fazer a demonstração comum e provar que se p(0)=p(1) portanto as demonstrações de existencia de subespaço para 0 são as mesmas que para 1.
Obrigado.
-
leandro_aur
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Dom Out 24, 2010 17:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciencia e Tecnologia
- Andamento: cursando
 por MarceloFantini » Dom Mar 04, 2012 19:50
por MarceloFantini » Dom Mar 04, 2012 19:50
Não entendi a sua colocação. O que provamos foi que, se
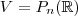
então
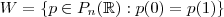
é subespaço.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por leandro_aur » Dom Mar 04, 2012 20:00
por leandro_aur » Dom Mar 04, 2012 20:00
Isso que eu quis dizer, não me expressei bem, my mistake...
-
leandro_aur
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Dom Out 24, 2010 17:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciencia e Tecnologia
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Subespaço Vetorial] Subespaço envolvendo matrizes
por hyge » Qua Mai 02, 2018 17:04
- 2 Respostas
- 10993 Exibições
- Última mensagem por adauto martins

Dom Mai 06, 2018 12:28
Álgebra Linear
-
- [Subespaço Vetorial] Verificar que é o conjunto é subespaço
por anderson_wallace » Seg Dez 30, 2013 17:56
- 3 Respostas
- 4693 Exibições
- Última mensagem por Renato_RJ

Ter Dez 31, 2013 14:00
Álgebra Linear
-
- subespaço vetorial
 por leobcastro » Seg Jun 16, 2008 10:18
por leobcastro » Seg Jun 16, 2008 10:18
- 8 Respostas
- 27000 Exibições
- Última mensagem por Heidji

Qua Jan 27, 2010 23:16
Geometria Analítica
-
- Subespaço vetorial
por drakonifor » Qui Mar 17, 2011 16:48
- 3 Respostas
- 3999 Exibições
- Última mensagem por LuizAquino

Qui Mar 17, 2011 18:39
Geometria Analítica
-
- subespaço vetorial
por amr » Seg Abr 18, 2011 10:56
- 3 Respostas
- 5253 Exibições
- Última mensagem por LuizAquino

Seg Abr 18, 2011 19:48
Introdução à Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
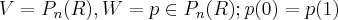


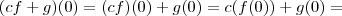
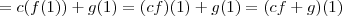 .
. e
e  pertencem ao espaço, sua avalição em zero é igual sua avalição em um.
pertencem ao espaço, sua avalição em zero é igual sua avalição em um.

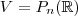 então
então 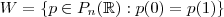 é subespaço.
é subespaço.
 .
.



