4-) Determinar o vetor x.(1, 4, -3)=7 e x(vetorial)(4, -2, 1)=(3, 5, -2).
Oi pessoal, to tentando resolver esse exercício mais não encontro saída em certo momento. Segundo a apostila o resultado é igual a (3, -1, 2).
eu fiz assim:
primeiro eu designei variáveis para os valores de x, ou seja, (a i, b j, c k)
o produto escalar do vetor x resultou em: (a +4b-3c)=7
e o produto vetorial: ((2c +b)i, (4c-a)j, (-2a-4b)k). depois eu coloquei esses valores em um sistema e é aonde surge o problema: 2c+b=3
4c-a=5
-4b-2a=-2
a solução que eu tentei foi somar esse sistema e para obter :(-3a-3b+6c)=6 e então relacionar com o produto escalar, ficou assim:
-3a-3b+6c=6
a +4b-3c=7
Já tentei fazer desta maneira e os valores das variáveis sempre resultam em zero.
Não tenho certeza se meu raciocínio chegou perto de estar certo....
Se poderem me ajudar... desde já agradeço!!!


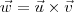 , então
, então 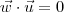 e
e 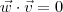 .
.

 .
.
 :
: