 por Ansso » Seg Out 18, 2010 22:22
por Ansso » Seg Out 18, 2010 22:22
Os pontos O = (0, 0), M= (raiz de 3, 1) , N e P = (0, p) são vértices consecutivos de um losango.
Sabendo-se que p > 0, pode-se concluir que o produto das coordenadas do ponto N é igual a
A)3 + raiz de 3 B) C) 6 D)6 + 2.raiz de 3 E) 12
Nessa questão ele da a figura do losango como no enuciado. So que quando vc desenha ele vai ter 2 coeficiente angular de tangencia 90°. O que faço com essa tangente? Utilizo ela como zero ou não existe mesmo?
Como resolver isso?
Obrigado pela Atenção!
-
Ansso
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Seg Out 18, 2010 22:17
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: formado
 por MarceloFantini » Ter Out 19, 2010 17:40
por MarceloFantini » Ter Out 19, 2010 17:40
Qual é a alternativa B?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Ansso » Ter Out 19, 2010 21:51
por Ansso » Ter Out 19, 2010 21:51
Ansso escreveu:Os pontos O = (0, 0), M= ( ?3, 1) , N e P = (0, p) são vértices consecutivos de um losango.
Sabendo-se que p > 0, pode-se concluir que o produto das coordenadas do ponto N é igual a
A)3 + ?3 B) 3?3 C) 6 D)6 + 2?3 E) 12
Nessa questão ele da a figura do losango como no enuciado. So que quando vc desenha ele vai ter 2 coeficiente angular de tangencia 90°. O que faço com essa tangente? Utilizo ela como zero ou não existe mesmo?
Como resolver isso?
Gabarito - B
Me confundir no gabarito Desculpem!
Obrigado pela Atenção!
Editado pela última vez por
Ansso em Ter Out 19, 2010 22:16, em um total de 1 vez.
-
Ansso
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Seg Out 18, 2010 22:17
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: formado
 por MarceloFantini » Ter Out 19, 2010 22:11
por MarceloFantini » Ter Out 19, 2010 22:11
Lembre-se que as diagonais de um losango são perpendiculares. Usando esse fato, a diagonal

é perpendicular a diagonal

. Equação da reta suporte de MN:
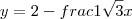
. Logo, a reta perpendicular e que passa por
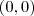
é
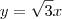
. Agora, como um losango tem lados iguais:
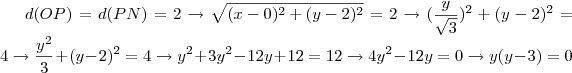
. Como nós queremos
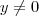
, sobra

, e portanto
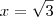
.
O produto
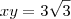
, alternativa B.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Ansso » Ter Out 19, 2010 22:35
por Ansso » Ter Out 19, 2010 22:35
Fantini escreveu:Lembre-se que as diagonais de um losango são perpendiculares. Usando esse fato, a diagonal

é perpendicular a diagonal

. Equação da reta suporte de MN:
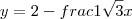
. Logo, a reta perpendicular e que passa por
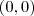
é
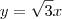
. Agora, como um losango tem lados iguais:
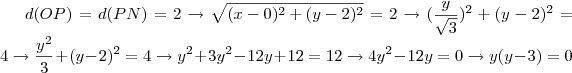
. Como nós queremos
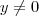
, sobra

, e portanto
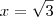
.
O produto
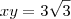
, alternativa B.
Não entendi o que vc fez com o p do verticie P(0,
p). Determinou algum valor? E essa parte "MN:
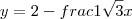
", tbm não sei de onde vc tirou.
Vc me deu uma outra visão mas só não conseguir entender esses 2 probleminhas ai.
E na alternativa ali eu me confundir.
Obrigado por ter Respondido!
-
Ansso
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Seg Out 18, 2010 22:17
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: formado
 por MarceloFantini » Ter Out 19, 2010 22:50
por MarceloFantini » Ter Out 19, 2010 22:50
Um losango tem os quatro lados iguais, então a distância de O até M é igual a distãncia de O até P, resulta em

. Sobre a reta MN é só pegar calcular o coeficiente angular com os pontos e ver onde corta o eixo y (no caso, justo no ponto P, logo em

).
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Ansso » Ter Out 19, 2010 23:04
por Ansso » Ter Out 19, 2010 23:04
É verdade, não tinha pensando nisso!!
Brigadão pela ajuda.

-
Ansso
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Seg Out 18, 2010 22:17
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Geometria Analítica
por maysa » Ter Abr 14, 2009 10:35
- 1 Respostas
- 7693 Exibições
- Última mensagem por Marcampucio

Ter Abr 14, 2009 15:52
Geometria Analítica
-
- GEOMETRIA ANALITICA
por GABRIELA » Ter Set 29, 2009 17:20
- 3 Respostas
- 5453 Exibições
- Última mensagem por GABRIELA

Qua Set 30, 2009 16:49
Geometria Analítica
-
- Geometria analítica
por shirata » Qua Nov 11, 2009 20:37
- 2 Respostas
- 4179 Exibições
- Última mensagem por shirata

Dom Nov 15, 2009 09:25
Geometria Espacial
-
- geometria analitica
por Jaison Werner » Sex Abr 23, 2010 21:19
- 3 Respostas
- 3961 Exibições
- Última mensagem por MarceloFantini

Dom Jun 13, 2010 19:03
Geometria Analítica
-
- geometria analitica
por Jaison Werner » Qui Abr 29, 2010 20:44
- 1 Respostas
- 2795 Exibições
- Última mensagem por MarceloFantini

Qui Abr 29, 2010 21:10
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




 é perpendicular a diagonal
é perpendicular a diagonal  . Equação da reta suporte de MN:
. Equação da reta suporte de MN: 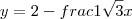 . Logo, a reta perpendicular e que passa por
. Logo, a reta perpendicular e que passa por 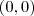 é
é 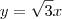 . Agora, como um losango tem lados iguais:
. Agora, como um losango tem lados iguais: 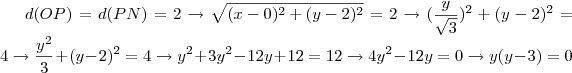 . Como nós queremos
. Como nós queremos 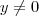 , sobra
, sobra  , e portanto
, e portanto 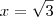 .
.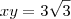 , alternativa B.
, alternativa B. . Sobre a reta MN é só pegar calcular o coeficiente angular com os pontos e ver onde corta o eixo y (no caso, justo no ponto P, logo em
. Sobre a reta MN é só pegar calcular o coeficiente angular com os pontos e ver onde corta o eixo y (no caso, justo no ponto P, logo em  ).
).


 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.