 . Escreva o vetor
. Escreva o vetor  como combinação linear dos vetores
como combinação linear dos vetores  e
e .
.Resumindo: eu tenho que escrever
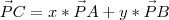 .
.Eu sei também que por conta dos ponto A B e C serem colineares eu posso escrever, por exemplo,
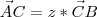 .
.Então. Eu tentei achar uma relações para que eu pudesse achar os escalares que multiplicam PA e PB mas não consegui achar. O que eu não estou conseguindo ver?
O mais proximo que eu consegui chegar da resposta foi
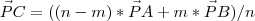 .
.http://i.imgur.com/pDxLyOi.jpg


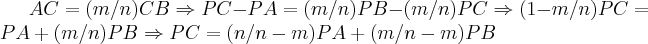

 e
e  se relacionam da forma
se relacionam da forma (1)
(1)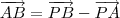 (2)
(2)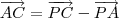 (3)
(3) e , portanto,
e , portanto,  , então, unindo tudo
, então, unindo tudo
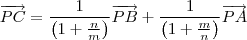

 PC-PA=(m/n)(PB-PC)=(m/n)PB-(m/n)PC
PC-PA=(m/n)(PB-PC)=(m/n)PB-(m/n)PC
 .
.
 :
: