 por matheus_frs1 » Dom Mai 11, 2014 00:34
por matheus_frs1 » Dom Mai 11, 2014 00:34
Determine o valor de m para que a circunferência de equação x²+y²-8x-my=-2 passe pelo ponto P=(8,-2).
Se vocês puderem não só jogar a resolução, mas me explicarem como devo fazer seria de uma grande ajuda.
Mt obrigado.
-
matheus_frs1
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Ter Mar 04, 2014 12:36
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Curso Técnico em Eletroeletrônica
- Andamento: cursando
 por Russman » Dom Mai 11, 2014 01:19
por Russman » Dom Mai 11, 2014 01:19
.
Editado pela última vez por
Russman em Dom Mai 11, 2014 01:21, em um total de 1 vez.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Russman » Dom Mai 11, 2014 01:19
por Russman » Dom Mai 11, 2014 01:19
Dizer que uma função qualquer

"passa pelo ponto" , por exemplo,

é o mesmo que dizer que

. Isto é, se você calcular a função em

vai obter

.
Exemplo:
Determine

tal que

passe pelo ponto
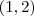
.
A forma mais simples de solucionar este problema é substituir

e

em

e obter uma equação em

. Veja:




Tente proceder da mesma forma para a circunferência. Você deve calcular, acho eu,

também! ( Feliz coincidência. hahah)
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por matheus_frs1 » Dom Mai 11, 2014 10:15
por matheus_frs1 » Dom Mai 11, 2014 10:15
Ah, jura que é só isso, Russman? Eu pensei que teria que achar a equação reduzida da circunferência e achar os valores a partir daí. Dessa maneira a gente cai em uma simples equação de primeiro grau, e realmente m = -3.
Obrigado pela ajuda, e só uma outra pergunta... toda questão desse tipo (determinar o parâmetro m) eu posso usar o mesmo raciocínio?
-
matheus_frs1
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Ter Mar 04, 2014 12:36
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Curso Técnico em Eletroeletrônica
- Andamento: cursando
 por Russman » Dom Mai 11, 2014 15:44
por Russman » Dom Mai 11, 2014 15:44
matheus_frs1 escreveu:Ah, jura que é só isso, Russman?
Acredito que seja. Foi a forma mais imediata que pensei.
matheus_frs1 escreveu:toda questão desse tipo (determinar o parâmetro m) eu posso usar o mesmo raciocínio?
Depende. Se for uma questão de "passar pelo ponto", na maioria das vezes é.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- geometria analitica-circunferencia
por xandeshaffer » Qua Set 12, 2012 19:33
- 1 Respostas
- 3162 Exibições
- Última mensagem por LuizAquino

Sex Set 14, 2012 16:14
Geometria Analítica
-
- geometria analitica circunferencia
por caciano-death » Sex Fev 05, 2016 21:30
- 0 Respostas
- 2011 Exibições
- Última mensagem por caciano-death

Sex Fev 05, 2016 21:30
Geometria Analítica
-
- [Geometria Analítica - Circunferência] Raio
por raimundoocjr » Dom Dez 16, 2012 18:14
- 2 Respostas
- 2967 Exibições
- Última mensagem por raimundoocjr

Dom Dez 16, 2012 19:37
Geometria Analítica
-
- Geometria Analitica - Circunferência - Duvida
por PiterPaulo » Sáb Mai 11, 2013 21:12
- 0 Respostas
- 1441 Exibições
- Última mensagem por PiterPaulo

Sáb Mai 11, 2013 21:12
Geometria Analítica
-
- [Geometria Analítica] Reta Tangente a Circunferência
por RasecAlmeida » Qui Out 16, 2014 13:57
- 1 Respostas
- 1812 Exibições
- Última mensagem por adauto martins

Sex Out 17, 2014 12:19
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




 "passa pelo ponto" , por exemplo,
"passa pelo ponto" , por exemplo,  é o mesmo que dizer que
é o mesmo que dizer que  . Isto é, se você calcular a função em
. Isto é, se você calcular a função em  vai obter
vai obter  .
. tal que
tal que  passe pelo ponto
passe pelo ponto 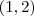 .
. e
e  em
em  e obter uma equação em
e obter uma equação em  . Veja:
. Veja:



 também! ( Feliz coincidência. hahah)
também! ( Feliz coincidência. hahah)







